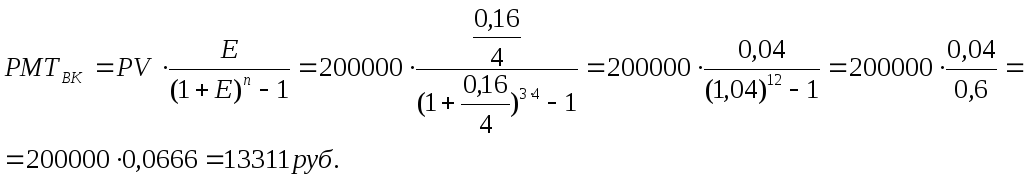|
|
Примеры: | контрольные | курсовые | дипломные | отзывы |
|
Временная стоимость в оценке стоимостиВременная стоимость денег в оценке недвижимостиДля определения стоимости собственности, приносящей доход, необходимо определить текущую стоимость денег, которые будут получены через какое-то время в будущем. В условиях инфляции очевидно, что деньги изменяют свою стоимость с течением времени. Основными операциями, позволяющими сопоставить разновременные деньги, являются операции накопления (наращивания) и дисконтирования. Накопление – это процесс приведения текущей стоимости денег к их будущей стоимости, при условии, что вложенная сумма удерживается на счету в течение определенного времени, принося периодически накапливаемый процент. Дисконтирование – это процесс приведения денежных поступлений от инвестиций к их текущей стоимости. В оценке эти финансовые расчеты базируются на сложном процессе, когда каждое последующее начисление ставки процента осуществляется как на основную сумму, так и на начисленные за предыдущие периоды невыплаченные проценты. Ниже рассматриваются шесть функций денег, о которых эксперт-оценщик должен знать и постоянно использовать их в практике. Денежные суммы. При оценке стоимости предприятия, приносящего чистый доход, важно определить денежные суммы, которые будут инвестированы в него и получены от этих инвестиций в процессе функционирования предприятия. Определение размеров этих денежных сумм позволит сделать заключение: обеспечат ли данные инвестиции положительную ставку дохода, т.е. такую ставку, при которой поступление денежных средств должно превышать их отток на покрытие будущих затрат. Время. Самое дорогое в этом мире это время: его нельзя вернуть. Вложенный в дело капитал со временем приносит процент, который, в свою очередь, со временем используется для получения еще большего процента. Время измеряется периодами или интервалами, которые составляют день, месяц, квартал, год и т.д. Риск. Под инвестиционным риском понимается неопределенность в получении чистых доходов от вложенных инвестиций. Ставка дохода. Ставка чистого дохода от инвестиций – это процентное отношение чистого дохода к вложенному капиталу. Ставка дохода предполагает оценку сумм ожидаемого чистого дохода и времени их получения. Ставка дохода на инвестиции часто называется ставкой конечной отдачи. Чистый доход определяется как чистая прибыль, полученная после уплаты налогов и других обязательных платежей, а также амортизационные отчисления и другие поступления. Аннуитет (обычный) — это серия равновеликих платежей, первый из которых осуществляется через один период, начиная с настоящего момента, т.е. платеж производится в конце рассматриваемых периодов. Сложный процент. Сложный (кумулятивный) процент означает, что полученный процент, положенный на депозит вместе с первоначальными инвестициями, становится частью основной суммы. В следующий период времени он, наряду с первоначальным депозитом, уже сам приносит процент. Простой процент не предполагает получение дохода с процента. Учеными разработаны специальные таблицы шести функций денежной единицы, помогающие экспертам-оценщикам вести расчеты с использованием сложных процентов. Таблицы состоят из шести граф (колонок), в которых помещены значения, полученные исходя из шести функций денежной единицы. Стандартные функции сложного процента для расчета денежных потоков. 1. Будущая стоимость денежной единицы. Эта функция, определяющая величину будущей стоимости сегодняшней денежной единицы (PV) через «n» периодов при сложном проценте равном «i»: FV=PV(1+i)n , (5.1) где: FV – накопленная (будущая) сумма после периода «n»; i– величина сложного процента; n– количество периодов накопления. 2. Текущая стоимость денежной единицы – величина, обратная будущей стоимости. Данная функция соответствует сегодняшней стоимости одной денежной единицы, полученной через «n» периодов при «i» процентах годовых:
3. Текущая стоимость обычного единичного аннуитета. Функция определяет настоящую стоимость серии будущих равных единичных платежей в течении «n» периодов при «i» процентах годовых. Использует коэффициент аннуитета или коэффициент Инвуда, определяемый как сумма коэффициентов настоящей стоимости единицы за «n» периодов при «i» процентах годовых:
4. Взнос на амортизацию денежной единицы. Определяет какой должен быть размер платежей в течение «n» периодов, чтобы их настоящая стоимость при норме процентов «i» была равна единице. Амортизация— в данном случае это погашение (возмещение, ликвидация) долга в течение определенного времени. Функция применяется при расчете платежей по погашению кредита, если эти платежи предполагаются одинаковыми по величине, при этом каждый платеж включает и выплату процента, и погашение по основной сумме кредита. Настоящую стоимость кредита можно рассчитать как сумму, превращающуюся в серию платежей величиной:
5. Будущая стоимость аннуитета. Показывает, какую будущую сумму даст единичный аннуитет при заданном числе периодов и норме процента. Практика депонирования одинаковых платежей и накопления их до определенной суммы широко распространена и называется формированием фонда возмещения. Величины коэффициентов будущей стоимости аннуитета рассчитываются по формуле:
С другой стороны, накопление единицы за период соответствует будущей стоимости величины настоящей стоимости единичного аннуитета в конце периода «n» и определяется по формуле: 6. Фактор фонда возмещения. Определяет величину платежа аннуитета, будущая стоимость которого через «n» периодов при заданной сумме процентов равна единице. Этот коэффициент дисконтирует будущую стоимость единичного фонда возмещения в серию равновеликих платежей. Применяется данная функция при расчете депонируемых платежей, которые должны сформировать к определенному моменту в будущем требуемый остаток на счете. Коэффициент фонда возмещения является обратныой величиной коэффициента будущей стоимости аннуитета.
Взаимосвязь функций сложного процента Все шесть стандартных функций сложного процента строятся на основе базовой формулы (1+i)n, которая описывает накопленную сумму денежной единицы. Поэтому все факторы являются производными от этого базового уравнения. Каждый из них предусматривает, что процент приносит деньги, находящиеся на депозитном счете, естественно, только до тех пор, пока они остаются на депозитном счете. Каждый из них учитывает эффект сложного процента. Три функции, как отмечалось выше, являются прямыми, три получают как обратные им величины. Расчеты, требующие умножения, выполняются и через деление на обратную величину и наоборот. Сумма фактора фонда возмещения и ставки периодического процента равна взносу на амортизацию единицы. Таким образом, взнос на амортизацию единицы является суммой двух величин, то есть заемщики выплачивают в течение срока кредита первоначальную сумму кредита и процент за кредит. В том случае, когда основная сумма кредита не амортизируется до истечения срока кредита и выплачивается только процент, заемщик может вносить на отдельный счет периодические платежи, рассчитанные по фактору фонда возмещения. Если фонд возмещения приносит процент по той же ставке, что и полученный кредит, то по окончании срока накопленная сумма может погасить остаток долга. Взнос на амортизацию единицы соотносится со ставкой процента так, чтобы взнос всегда превышал периодическую ставку процента вне зависимости от срока кредита. Текущая стоимость обычного аннуитета никогда не может превысить фактор, равный частному от деления 1 денежной единицы на периодическую ставку процента. Например, если годовая ставка равна 10%, то максимальное значение рассчитывается: 1 д.е.: 0,1 = 10. Максимальное значение этого фактора при любой ставке процента показывает сумму, достаточную для генерирования 1 д.е. за период на протяжении неограниченного времени. Остаток 10 д.е. при 10%-й ставке принесет за год 1 д.е. процента. Контрольные вопросы для самопроверки 1. С чем связана необходимость корректировки денежных потоков возникающих в различное время? 2. Какие параметры влияют на стоимость денежных потоков в различное время? 3. Какие параметры необходимо корректировать, если периодичность начисления процентов отличается от года? 4. Какая функция используется для расчёта платежей за погашение кредита? 5. Какая функция используется для соотнесения стоимости бедующих регулярно поступающих платежей от объекта недвижимости с ценой его приобретения? Время между датами, оформление векселей в финансовой математикеКогда временной интервал дается не явно, а в форме промежутка между датами, обычно вычисляют точное число дней, включая первый или последний день, но не оба. Такой способ определяет так называемое точное время. Его легко определить, если обе даты относятся к одному и тому же году и имеется в наличии календарь, показывающий порядковый номер каждого дня года. Тогда достаточно из порядкового номера поздней даты вычесть порядковый номер ранней даты и результат даст продолжительность периода. В високосных годах порядковый номер дня после 28 февраля следует увеличивать на единицу. Упомянутый здесь календарь порядковых номеров дней года обычно содержится среди таблиц для финансовых расчетов, имеющихся в руководствах по финансовым и коммерческим расчетам. Другой способ подсчета количества дней между датами основан на предположении, что каждый месяц года состоит из 30 дней. Когда используется этот способ, получающийся результат называется приближенным временем. Независимо от того, каким образом рассчитывалось число дней временного периода, могут начисляться обыкновенные или точные простые проценты. Поэтому возможны четыре различных варианта числового выражения простого процента. Сочетание точного времени и точного простого процента практически не встречается. Чаще всего встречается случай, когда используется точное время и обыкновенный простой процент. Этот вариант часто называется правилом банкиров. В дальнейшем мы будем всегда подразумевать именно этот способ расчетов, если не будет оговорено другое. ПРИМЕР 1 Ссуда была выдана 10 марта и возвращена 17 ноября. Найти a) точное время, b) приближенное время периода. РЕШЕНИЕ a) 10 марта
является 321 - 69 = 252. b) При определении приближенного времени для удобства составим следующую табличку 9
Разность равна 8 месяцев и 7 дней или 247 дней, если считать, что в каждом месяце по 30 дней. ПРИМЕР 2 Ссуда была выдана 20 октября 1993 года и возмещена 15 июня 1995 года. Найти a) точное время, b) приближенное время периода. РЕШЕНИЕ a) 20 октября
является 72 + 365 + 166 = 604 дня. b) При определении приближенного времени опять обращаемся к использованию вспомогательной таблицы
Приближенное время периода равно 1 год 7 месяцев и 25 дней или 360 + 210 + 25 = 595 дней. Оформление денежных отношений между партнерами финансовой сделки может производиться при помощи векселей (расписок), которые, по существу, являются письменными обязательствами заплатить определенную сумму денег в установленный срок. Дата, до которой деньги должны быть выплачены, называетсядатой погашения. Сумма денег, которая должна быть выплачена, называетсясуммой погашения. Хотя эти две характеристики являются наиболее существенными, обычно в тексте расписки содержится и другая информация, которая может оказаться необходимой. Во всяком случае, текст векселя должен быть составлен таким образом, чтобы на его основании дата и сумма 10 погашения могли бы быть однозначно определены. Например, предположим, что некто Иванов занял у Петрова 4000 рб и согласился вернуть долг с 76 рб процентов через 4 месяца. Тогда Иванов мог бы дать Петрову следующий вексель : **************************************************************** 10 октября 1994 г. Через четыре месяца после указанной даты я обязуюсь по требованию Петрова заплатить сумму 4000 рб и простые проценты в размере 5,7% годовых. (Подпись) Иванов **************************************************************** Такой вексель является обязательством Иванова заплатить
Петрову 4076 рб 10 февраля 1995 г. Сумма 4000 рб называется лицевой суммой векселя, а **************************************************************** 10 октября 1994 г. Через четыре месяца после указанной даты по требованию Петрова я обязуюсь заплатить сумму 4076 рб без процентов. (Подпись) Иванов ********************************************************** Когда срок векселя дан в месяцах, он обычно погашается в тот же самый день соответствующего месяца. Исключение составляет случай, когда дата погашения попадает на число месяца, которое не существует (например, 31 июня или 30 февраля). Тогда датой погашения считается последний день месяца. Если же срок векселя дан в днях, обычно рассчитывается точная дата выплаты занятых денег. Например, 80дневный вексель, датированный 16 ноября, погашался бы 4 февраля. При таких расчетах снова был бы полезен календарь с порядковыми номерами дней года. ПРИМЕР 3 Установить дату
погашения РЕШЕНИЕ 17 июля
является 11 Датированные суммы - финансовая математикаИспользование значений денежных сумм без указания даты, когда они
обязательно знать норму процента. Если человек имеет возможность в
так как после получения через три года 1000 рб можно в
течение следующих четырех лет при норме 8% годовых накопить 1360,49 рб. Точно
также 793,83 рб, ( = 1000 ? (1,08) В общем случае датированные суммы сравниваются по следующему правилу эквивалентности: сумма P , полагающаяся на данную дату, эквивалентна при данной норме сложного процентаi суммеS , полагающейся наn периодов конверсии позже, если является справедливым хотя бы одно из следующих равенств: S = P(1 +i)п илиP =
S(1 +i) Таким образом, накопление или дисконтирование могут рассматриваться как простое преобразование заданной датированной суммы к другой дате. Преобразование делается в соответствии со следующей временной диаграммой:
27  Прошлая и будущая суммы эквивалентны датированной сумме D. Важным и полезным свойством эквивалентных датированных сумм является следующее свойство 1 : при данной норме сложного процента еслиA эквивалентноB иB эквивалентноC , тоA эквивалентноC. Для доказательства этого утверждения мы расположим данные на временной диаграмме следующим образом :
Если A эквивалентноB
, тоB = A(1 +i) Исключая из этих равенств сумму B , получим, что C = A(1 +i) Полученный результат является условием эквивалентности датированных сумм A иC. Это свойство не имеет места для норм простого процента и норм простого дисконта. Поэтому понятие эквивалентности для этих норм не применяется. ПРИМЕР 1 Долг 10000 рб следует выплатить через 10 лет. Если деньги стоятj1 = 5% , найти эквивалентный долг через a) 1 год , b) 15 лет. РЕШЕНИЕ Построим временную диаграмму
Согласно правилу эквивалентности X = 10000 ? (1,05) 28  Y = 10000 ? (1,05)5 = 12762,8 полагается через 15 лет
11956,2 X Здесь 6 и 16 представляют количества полугодовых периодов начисления, начиная с начального момента. Искомая сумма получается путем накопления основной суммы 11956,2 рб за 10 периодов начисления при норме 2% за период, то есть X = 11956,2 ? (1,02)10 = 14574,5 полагается через 8 лет. Нормы временного предпочтения6.1. В сфере оценки стоимости природных ресурсов процедуры дисконтирования, определения величины коэффициента капитализации и ставок дисконтирования носят дискуссионный характер из-за высокой неопределенности и субъективности выбираемых параметров и занижения стоимости объекта оценки. Для обозначения явления занижения стоимости в результате дисконтирования введен термин «тирания дисконтирования» или «диктатура дисконтирования», который означает безосновательное уменьшение стоимости или обесценивание природного ресурса, в том числе земли, из-за использования определенной техники математического расчета. Например, стоимость лесных земель после вырубки леса принимает нулевое значение, так как срок получения следующего дохода от вырубки в среднем составляет 50-100 лет, а стоимость будущего леса обесценивается из-за применения высоких ставок дисконтирования. 6.2. Для решения проблемы дисконтирования при оценке природных объектов используются следующие приемы: - проводится более полный учет экономической ценности благ, продуцируемых этими объектами; - проводится более полный учет экологических ущербов; - устанавливаются социальные нормы временного предпочтения (более низкие ставки дисконтирования по сравнению с рыночным сектором); - увеличивается период капитализации доходов и расходов, то есть период анализа потока денежных средствпродлевается за пределы нормального периода жизни проекта на дополнительное число лет. 6.3. В качестве социальных норм временного предпочтения в мировой практике используются ставки дисконтирования в 2-4%, а иногда и ниже. Типичным примером использования в расчетах стоимости социальных норм временного предпочтения является кадастровая оценка сельскохозяйственных угодий, когда в качестве периода капитализации применяется период в 33 года, что соответствует ставке дисконтирования в 3% (1/33?100%=3%). 6.4. Коэффициент капитализации при оценке экономической ценности природных объектов, можно рассчитывать как величину обратную периоду естественного или искусственного восстановления природной экосистемы. Например, в качестве периода восстановления лесной экосистемы можно использовать период достижения лесом возраста спелости. Допустим, срок восстановления леса (лесной экосистемы) составляет 70 лет. Тогда коэффициент капитализации равен: 1/70 = 0, 014. В этом случае коэффициент капитализации представляет норму возврата «биологического капитала». 6.5. Одним из вариантов определения таких периодов может
стать их расчет через определение отношения запаса биомассы экосистемы
(углерода) к ее годовому приросту, взвешенному по основным структурным
элементам экосистемы: 6.6. В этом случае коэффициент капитализации определяется
как величина обратная периоду накопления углерода в экосистеме 6.7. Так как соотношение между запасом биомассы и ее годовым приростом является константой для основных типов природных экосистем, то для практических расчетов можно рекомендовать следующие периоды восстановления и коэффициенты капитализации, рассчитанные для основных природных зон России исходя из этих показателей:
Стоимость денег во времени в финансовой математикеКонцепция стоимости денег во времени основывается на двух предпосылках: •инвестиции должны приносить доход, •деньги полученные в настоящем, имеют большую стоимость, чем деньги, которые могут быть получены в будущем.
 Учет фактора времени при оценке стоимости бизнесаВ результате освоения темы студент должен знать: временную концепцию денег. уметь: применять методы наращения и дисконтирования. владеть: техникой вычисления простого и сложного процента. Основные вопросы, подлежащие изучению в данной теме: Учёт фактора времени при оценке денежных потоков. Причины изменения стоимости (покупательной способности) денег во времени. Понятие простого и сложного процента. Будущая и текущая стоимость денежной единицы. Текущая стоимость аннуитета. Будущая стоимость аннуитета. Периодический взнос в погашение кредита. Выполнение вычислений с помощью таблиц функций сложного процента. Самостоятельная работа студентов заключается в нахождение ответов на следующие вопросы: 1. Почему денежные потоки, возникающие в различные периоды времени не сопоставимы по своей величине? 2. Назовите прямые и обратные функции сложного процента. 3. Приведите примеры денежного потока, называемого аннуитетом. 4. В чём отличие обычного аннуитета от авансового? 5. Приведите примеры применения отдельных функций сложного процента при оценке стоимости предприятия. План практического занятия:
2. Решение задач на нахождение сегодняшней и будущей стоимости денег, т.е. на процесс наращения и дисконтирования. Учет фактора времени при оценке стоимости бизнеса предприятияВремя является особым экономическим ресурсом. Люди в своей производственно-экономической деятельности располагают ограниченным количеством этого невоспроизводимого ресурса. Однако время довольно редко причисляется к числу экономических ресурсов (его не надо добывать) и рассматривается в качестве такового, хотя используется понятие «ресурс времени». Между тем время — наиболее универсальный ресурс, без наличия которого не протекает ни один экономический процесс. Производители вынуждены вначале приобретать необходимые ресурсы, осуществлять затраты, чтобы создать факторы производства. Лишь затем они возмещают эти затраты продажей продукта, произведенного с использованием этих факторов. То есть в экономике неизбежно приходится вначале вкладывать в дело средства, создавать условия протекания производственных процессов и только потом получать желаемый результат, отдачу от вложенных средств. Промежуток времени между вложением средств, вовлечением ресурсов и их превращением в действующие факторы производства может существенно различаться для разных факторов производства и стадий воспроизводства. Источником прироста капитала и движущим мотивом осуществления инвестиций являётся получаемая от них прибыль. Эти два процесса — Вложение капитала и получение прибыли — могут происходить в различной временной последовательности: а) последовательное протекание процессов вложения капитала и получения прибыли — прибыль получается сразу после завершения инвестиций в полном объеме; б) параллельное протекание процессов вложения капитала и получения прибыли — получение прибыли возможно еще до полного завершения процесса инвестирования; в) интервальное протекание процессов вложения капитала и получения прибыли — между периодом завершения инвестиций и получением прибыли проходит определенное время (временной лаг). Поэтому одна из главных проблем экономической оценки инвестиций состоит в том, чтобы сопоставить выплаты, которые делаются в разные моменты времени, так как одинаковые по величине затраты, осуществляемые в разное время, экономически неравнозначны. Одна из базовых концепций экономики предприятия состоит в том, что стоимость определенной суммы денег — это функция от времени возникновения денежных доходов или расходов. Рубль, полученный сегодня, стоит больше рубля, который будет получен в будущем. 2.2. ОЦЕНКА СТОИМОСТИ ДЕНЕГ ВО ВРЕМЕНИ Экономическая оценка инвестиций требует осуществления различного рода финансово-экономических расчетов, связанных с потоками денежных средств в разные периоды времени. Ключевую роль в этих расчетах играет оценка стоимости денег во времени. Одна из базовых концепций экономики коммерческого предприятия и теории принятия управленческих решений состоит в том, что стоимость определенной суммы денег — это функция от времени возникновения денежных доходов или расходов.То есть стоимость денег с течением времени изменяется с учетом нормы прибыли на денежном рынке, в качестве которой может выступать норма ссудного процента (или процента). В данном случае под процентомпонимается сумма доходов от использования денег на денежном рынке. Учитывая, что инвестирование представляет собой обычно длительный процесс, в оценке инвестиций часто приходится сравнивать стоимость денег в начале их инвестирования со стоимостью денег при их возврате в виде будущей прибыли, амортизационных отчислений и т.п. В практике экономических расчетов влияние разновременности затрат и результатов учитывается путем приведения по шкале времени. Приведение по шкале времени может осуществляться на основе процессов наращения и дисконтирования. Наращение — это процесс определения возвращаемой (будущей) суммы денежных средств, если известны исходная сумма вложений, процентная ставка дохода от них и период накопления. Дисконтирование — процесс приведения денежных сумм, получаемых в будущем, к более раннему (начальному) моменту времени. Таким образом, в процессе сравнения стоимости денежных средств при их инвестировании и возврате принято использовать два основных понятия: — будущая стоимость денег, FV; — настоящая (текущая, современная) стоимость денег, PV. Фактор фонда возмещения - функция временной стоимости денегФактор фонда возмещения показывает денежную сумму, которую необходимо депонировать в конце каждого периода для того, чтобы через заданное число периодов остаток составил 1 долл. Данный фактор принимает во внимание процент, получаемый по депозитам. Например, для того чтобы через четыре года получить 1 долл. При нулевом проценте, в конце каждого года необходимо депонировать 25 центов. Если же сложная ставка составит 10%, то по окончании каждого из четырех лет необходимо будет депонировать только 0,215471 долл. Разница между 1 долл. И суммой четырех взносов (4 X 0,215471 = 0,861884) равна проценту, приносимому депозитом. Предположим, что студентка хочет скопить за четыре года 4641 долл., депонируя по окончании каждого года равные суммы. В том случае, если остаток на депозите ежегодно приносит 10%, то обязательный ежегодный взнос должен составлять 1000 долл. (0,215471 х 4641 = 1000 долл.). Часто в тех случаях, когда вплоть до истечения срока долгового обязательства кредитору выплачивается только процент, заемщики для погашения основной суммы кредита создают специальные фонды возмещения. В каждый период должник вносит в отдельный фонд сумму, которая вместе с начисляемым на нее процентом должна обеспечить погашение основной части кредита. С истечением срока задолженности фонд закрывается, а его остаток используется для погашения кредита. Фактор фонда возмещения показывает сумму, которая должна быть депонирована в каждый период для того, чтобы по истечении заданного числа периодов остаток достиг 1 долл. Это величина, обратная фактору накопления единицы за период. Фактор фонда возмещения составляет часть от взноса на амортизацию 1 долл. Последний равен сумме двух коэффициентов. Первый — ставка процента, или дохода на инвестиции. Второй — фактор фонда возмещения, возмещение или возврат инвестированных средств. Фактор фонда возмещения, рассчитанный по тому же проценту, что и ставка по кредиту, является нормой погашения основной суммы кредита. Например, фактор взноса на амортизацию кредита в 1 долл. При 10%-ной ставке в течение четырех лет составляет 0,315471. Из этого фактора 0,10 приходится на 10%-ную ставку (0,10) и 0,215471 — на фактор фонда возмещения при 10%-ной ставке. Если процент по кредиту должен выплачиваться ежегодно, а в фонд возмещения в каждый период вносятся 0,215471 долл., приносящие 10%, то через четыре года в фонде будет накоплена сумма, как раз достаточная для погашения 1-долларового кредита. Расчеты показаны в табл. 4-3. Фактор фонда возмещения описан графически на рис. 4-5. Предварительно рассчитанные таблицы Для факторов фонда возмещения также построены таблицы. Цифра на пересечении числа периодов и соответствующей колонки (колонка 3 таблиц в Приложении Б) показывает, какими должны быть равновеликие периодические платежи при выбранной ставке процента для того, чтобы по окончании всего срока на счету аккумулировался 1 доллар. При расчете таблиц использована формула:
где: n- число периодов; Е - периодическая ставка процента
Фонд возмещения капитала определяется по формуле:
где: РМТВК – фонд возмещения капитала; PV –возмещаемый капитал. Пример 2.8.Судовладелец определил, что на ремонт судна через три года потребуется 200 000рублей. Какую сумму необходимо откладывать ежеквартально в банк под 16 % годовых, чтобы накопить ремонтный фонд к указанному сроку? Решение:
Элементы финансовой математики в оценке стоимости (временная оценка денежных потоков)ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ Накопление – это процесс приведения текущей стоимости денег к их будущей стоимости, при условии, что вложенная сумма удерживается на счету в течение определенного времени, принося периодически накапливаемый процент. Дисконтирование – это процесс приведения денежных поступлений от инвестиций к их текущей стоимости. Аннуитетные платежи (PMT) – это серия равновеликих платежей (поступлений), отстоящих друг от друга на один и тот же промежуток времени. Выделяют обычный и авансовый аннуитеты. Если платежи осуществляются в конце каждого периода, то аннуитет обычный, если в начале – авансовый. Текущая стоимость (PV) (англ. Present value) - исходная сумма долга или оценка современной величины денежной суммы, поступление которой ожидается в будущем, в пересчете на более ранний момент времени. Будущая стоимость (FV) (англ. Future value) - сумма долга с начисленными процентами в конце срока. Ставка дохода или процентная ставка (i) (англ. Rate of interest) - является относительным показателем эффективности вложений (норма доходности), характеризующим темп прироста стоимости за период. Срок погашения долга (n) (англ. Number of periods) - интервал времени, по истечении которого сумму долга и проценты нужно вернуть. Срок измеряется числом расчетных периодов, обычно равных по длине (например, месяц, квартал, год), в конце которых регулярно начисляются проценты. Частота накоплений в год (k) - периодичность начисления процентов оказывает влияние на величину накопления. Чем чаще начисляются проценты, тем больше накопленная сумма. ОБОЗНАЧЕНИЯ К ФОРМУЛАМ FV – будущая стоимость денежной единицы; PV – текущая стоимость денежной единицы; PMT – равновеликие периодические платежи; i – ставка дохода или процентная ставка; n – число периодов накопления, в годах; k – частота накоплений в год. Для понимания сущности методов оценки доходной недвижимости необходимо рассмотреть функции сложного процента, которые характеризуют количественные изменения стоимости денег во времени. Базовая аксиома всей методологии оценки недвижимости – «деньги завтра не есть деньги сегодня». Приведение денежных сумм, возникающих в разное время, к сопоставимому виду называется временнoй оценкой денежных потоков. Временная оценка денежных потоков основана на использовании шести функций сложного процента или шести функций денежной единицы. Для операций финансового анализа используются специальные таблицы шести функций, содержащие предварительно рассчитанные по сложному проценту факторы: колонка 1 — накопленная сумма (будущая стоимость) денежной единицы (fvf, i, n); колонка 2 — накопление денежной единицы (fvaf, i, n); колонка 3 — фонд возмещения (sff, i, n); колонка 4 — текущая стоимость единицы (реверсии) (pvf, i, n); колонка 5 — текущая стоимость обычного аннуитета (pvaf, i, n); колонка 6 — взнос на амортизацию единицы (iaof, i, n). Таблицы, рассчитанные для годового и ежемесячного начисления процента, приведены в приложении. Порядок использования таблиц: 1. Выбрать раздел ежегодного или ежемесячного учета накопления. 2. Найти страницу с соответствующей ставкой сложного процента. 3. Найти колонку, где указывается величина соответствующего фактора сложного процента. 4. Найти продолжительность расчетного срока в левой или число периодов в правой колонке выбранной таблицы. 5. Найти расчетную величину фактора сложного процента на пересечении соответствующей колонки и ряда таблицы. 6. Умножить величину единичного фактора на известную исходную денежную сумму, соответствующую данной ситуации в задаче. В предварительно разработанных таблицах шести функций сложного процента данный фактор следует искать в первой колонке таблицы. Список литературы и источников на тему "Временная стоимость в оценке стоимости"
Другие похожие работы |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
© 2002 - 2024 RefMag.ru |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
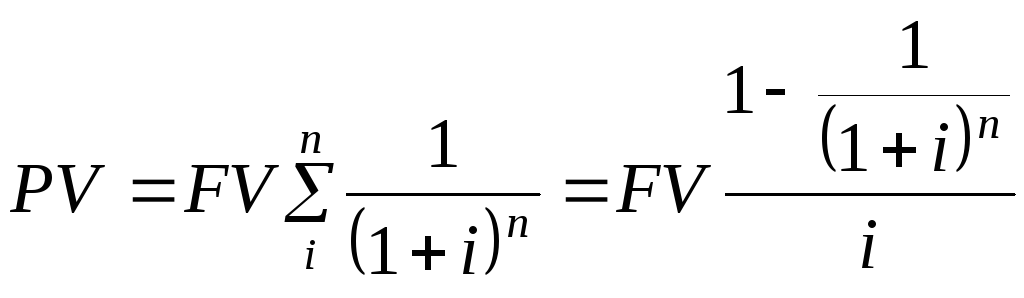 (5.3)
(5.3)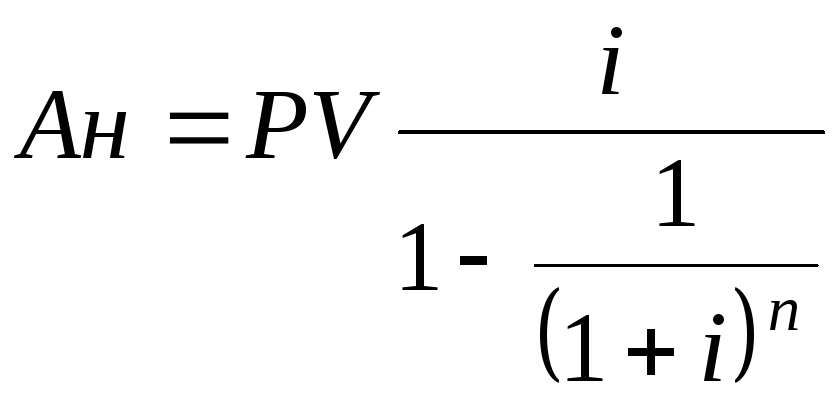 (5.4)
(5.4)