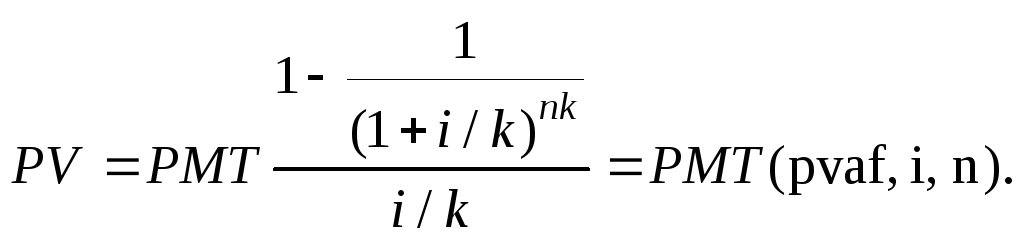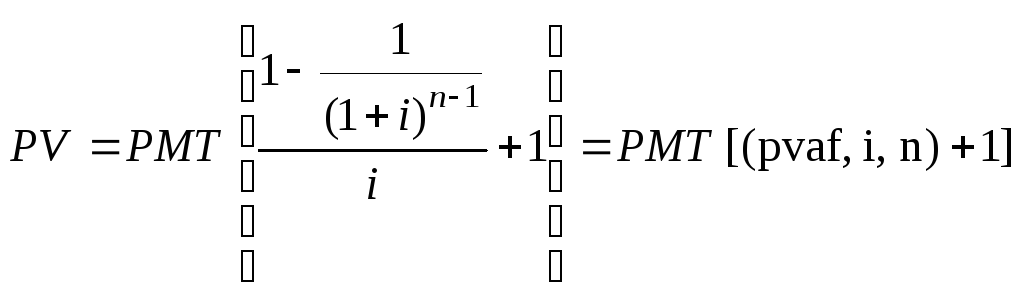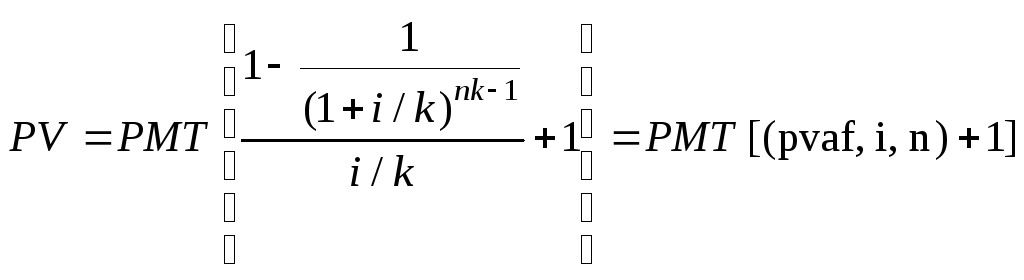|
|
Примеры: | контрольные | курсовые | дипломные | отзывы |
|
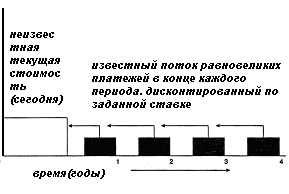
Текущая стоимость в оценочной деятельностиОпределение текущей стоимости при оценке бизнеса предприятияPV (1 1r) FV •PV – текущая стоимость в остаточный период •FV – будущая стоимость в остаточный период Текущая стоимость аннуитета - функция временной стоимости денегОбычный аннуитет определяется как серия равновеликих платежей, первый из которых осуществляется через один период начиная с настоящего момента. Он также определяется как серия поступлений. Например, право получать 100 долл. В конце каждого года в течение следующих 4 лет создает обычный аннуитет. Текущая стоимость аннуитета показана графически на рис. 2.3.
Рис. 2.3. Текущая стоимость обычного аннуитета Текущая стоимость аннуитета при заданной ставке дисконта может быть рассчитана путем оценки каждого платежа (поступления) в отдельности. При этом сумма каждого платежа умножается на соответствующий фактор текущей стоимости единицы. Например, право получения 100 долл. Чистого рентного дохода в конце каждого года на протяжении следующих 4 лет может быть оценено, если учитывать каждое из четырех поступлений как отдельную реверсию. При 10%-ной ставке дисконта стоимость первого поступления равна 90,91 долл. (100,00 долл. X 0,90909.- 90,91 долл.); второго — 82,64 долл., третьего — 75,13, четвертого — 68,30 долл. Текущая стоимость всего четырехлетнего аннуитета составляет 316,98 долл. (90,91 долл. + 82,64 долл. + 75,13 долл. + 68,30 долл.). Поэтому при 10%-ной ставке сегодняшние инвестиции в 316,98 долл. (текущая стоимость) являются обоснованной платой за право ежегодного получения 100,00 долл. На протяжении последующих четырех лет. Предварительно рассчитанные таблицы. Широкое и интенсивное использование фактора текущей стоимости аннуитета привело к построению соответствующих таблиц. Данные таблицы показывают факторы с учетом того, что каждый платеж за период равен 1 долл. Это факторы аннуитета (annuity factors), или факторы Инвуда (Inwood factors), по имени Уильяма Инвуда (1771—1843). Во многих таблицах сложного процента они показаны в колонке 5. Фактор Инвуда рассчитывается по следующей формуле:
Фактор текущей стоимости аннуитета может быть также рассчитан как сумма текущих стоимостей в 1 долл. За определенный временной период
Для построения аннуитетной таблицы следует просто сложить факторы текущей стоимости единицы за соответствующее число лет, как это показано в табл. 2.2. ТАБЛИЦА 2.2 Соотношение текущей стоимости единицы и текущей стоимости аннуитета (ставка * 10%)
Определив фактор текущей стоимости аннуитета можно определить текущую стоимость денежного потока платежей по формуле:
где: PV?, PVA- текущая стоимость аннуитета; РМТ- единовременный денежный платеж в периоде; aN, % - фактор текущей стоимости аннуитета. Пример 2.5. Оставшийся срок полезного использования судна составляет шесть лет, в течение которых владелец рассчитывает получать в виде арендных платежей 400 000 рублей ежегодно. За какую минимальную сумму может быть продано судно сегодня при условии, что ставка дисконтирования (норма прибыли на капитал) равняется 14%? Решение:
Текущая стоимость аннуитета и ее использование для целей оценки стоимостиАннуитет— серия равных платежей, вносимых или получаемых через равные промежутки времени в течение определенного периода. В том случае, если платежи (поступления) производятся в конце каждого периода, говорят обобычном аннуитете. Если же платежи (поступления) осуществляются авансом, т.е. в начале каждого периода, говорят обавансовом аннуитете. Базовые формулы: а где PMT -равновеликие периодические платежи (поступления); б) при более частых, чем 1 раз в год, платежах (поступлениях):
Расчет текущей стоимости авансового аннуитета. а) при платежах (поступлениях) в начале каждого года:
для (n-1)-го периода; б) при более частых, чем 1 раз в год, платежах (поступлениях):
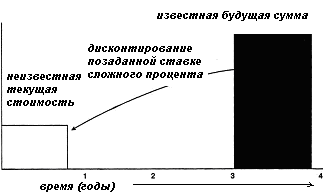
для (n-1)-го периода. Текущая стоимость единицы - функция временной стоимости денегТекущая стоимость единицы ( реверсии)— это величина обратная накопленной сумме единицы. Это текущая стоимость одного доллара, который должен
Рис. 2.2. Текущая стоимость реверсии быть получен в будущем. Поскольку целью осуществления инвестиций является получение доходов в будущем, умножение фактора текущей стоимости реверсии на величину ожидаемого будущего дохода является важнейшим шагом в оценке инвестиций. Текущая стоимость реверсии (Vn)описана графически на рис. 2.2. Данный коэффициент используется для оценки текущей стоимости известной (или прогнозируемой) суммы будущего единовременного поступления денежных средств с учетом заданного процента. При применении фактора текущей стоимости используются понятия дисконтирование (discounting) или ставка дисконта (discount rate), противоположные понятиям накопление (compounding) и ставка процента (interest rate), применяемым при расчете накопленной суммы единицы. Поскольку деньги обладают стоимостью во времени, один доллар, который будет получен в будущем, стоит меньше доллара, получаемого сегодня. Насколько меньше (сумма дисконта), зависит от: а) разрыва во времени между оттоком и притоком денежных средств и б) необходимой ставки процента или дисконта. Например, при 10%-ной ставке процента (ставке дисконта) текущая стоимость 100,00 долл., ожидаемых к получению через год, равна 90,91 долл. Арифметическая проверка: если сегодня инвестор вкладывает 90,91 долл. И в течение следующего года может получить чистый доход в 9,09 долл., то процент составит 9,09 долл.; поэтому через год основная сумма инвестиций, включая добавленный процент, будет равна 100,00 долл. (90,91 долл. + 9,09 долл. = 100,00 долл.). Инвестор, который рассчитывает получить через два года 100,00 долл. И вкладывает сегодня 82,64 долл., получит 10%-ную годовую ставку. Проверка: при 10%-ной годовой ставке 82,64 долл. Превратятся через год в 90,91 долл., а через 2 года — в 100,00 долл. Поэтому формула текущей стоимости денег:
где: где: FV- будущая стоимость денег; PV- текущая стоимость денег; (1+E)n – фактор сложного процента;
Формула расчета коэффициента текущей стоимости (реверсии) имеет следующий вид:
Данный фактор является обратной величиной от накопленной суммы единицы. Поэтому любая задача, которая может быть решена с использованием фактора накопленной суммы единицы, может быть также решена с применением фактора реверсии, однако не через умножение, а через деление. Например, как показано ранее, 100,00 долл., накапливаемые по сложной ставке 10%, через пять лет возрастут до 161,05 долл. Поскольку 100,00 долл. Через пять лет превратятся в 161,05 долл., то 62,05 долл. — это та сумма, которая за пять лет возрастет до 100,00 долл. Пример 2.4. Покупатель земельного участка рассчитывает перепродать его через 7 лет за 100 000 рублей. Какова максимальная сумма, которую он может предложить продавцу, если хочет, чтобы его годовой доход составил 15 % ? Решение:
Текущая стоимость единицы (реверсии) и ее использование для целей оценки стоимостиа) При начислении процентов 1 раз в год:
б) при более частом, чем 1 раз в год, начислении процентов:
Смысл задач такого класса состоит в том, чтобы при заданной ставке дисконта дать оценку текущей стоимости тех денег, которые могут быть получены (заплачены) в конце определенного периода. Формулы современной (текущей) величины стоимостиОбычная годовая рента Пусть член годовой ренты равен R, процентная ставкаi, проценты начисляются один раз в конце года, срок рентыn. Тогда дисконтированная величина первого платежа равна R1+1 i = Rv, где 1 v = 1+ i - дисконтный множитель. Приведенная к началу ренты величина второго платежа равна Rv2 и т.д. В итоге приведенные величины образуют геометрическую прогрессию:Rv, Rv2, Rv3, ..., Rvn, сумма которой равна
где
(1.8) (1.9) - коэффициент приведения ренты. Как видим, коэффициент приведения ренты зависит только от двух параметров: срока ренты n и процентной ставкиi. Поэтому его значения могут быть представлены в табличном виде. Такие таблицы можно найти в книгах или построить самим на компьютере. Рента Аналогичные рассуждения позволяют получить формулу для расчета современной величины ренты в самом общем случае для произвольных значений p иm
от которой нетрудно перейти к частным случаям при различных p иm. Список литературы и источников на тему "Текущая стоимость в оценочной деятельности"
Другие похожие работы |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
© 2002 - 2024 RefMag.ru |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
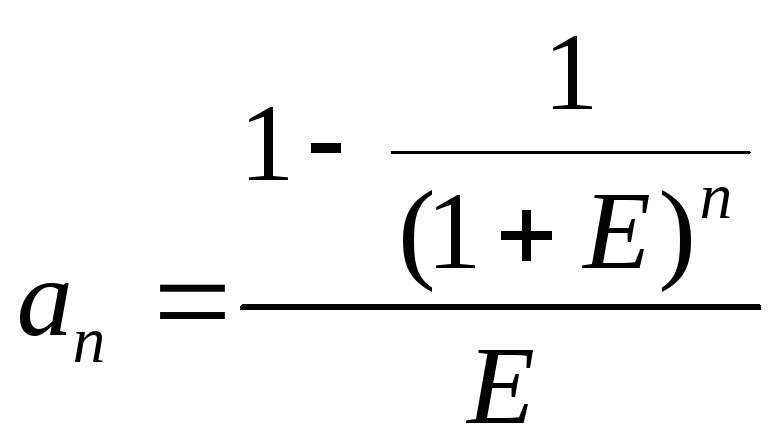
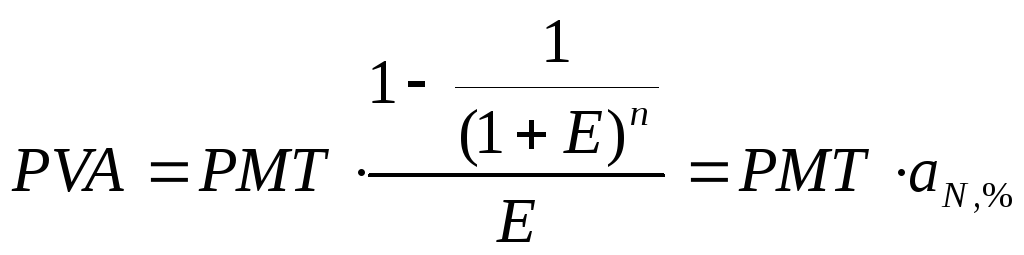
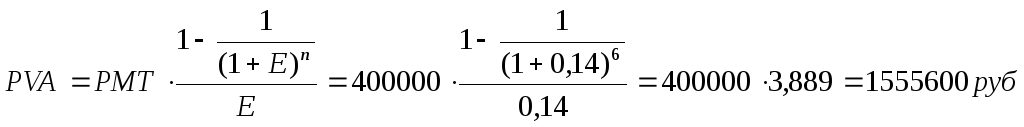
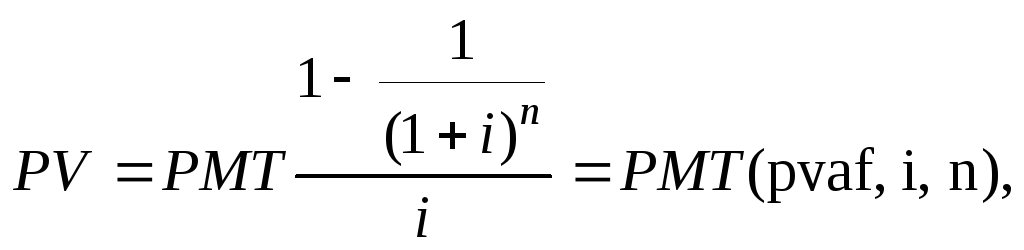 ) при платежах (поступлениях) в конце каждого года:
) при платежах (поступлениях) в конце каждого года: