|
|
Примеры: | контрольные | курсовые | дипломные | отзывы |
|
Регрессионная статистика в оценке стоимостиВид представления дополнительной регрессионной статистики в сравнительном подходе оценки недвижимости
Таблица 41 Дополнительная регрессионная статистика в сравнительном подходе оценки недвижимости
Таблица 42 Дополнительная регрессионная статистика для целей оценки недвижимости
Таблица 42 Допущения и ограничительные условия, использованные при проведении исследования по оценке стоимости предприятия бизнесаСледующие допущения и ограничивающие условия являются неотъемлемой частью данного отчета. В процессе подготовки настоящего отчета, оценщик исходил из достоверности представленных документов. Отчет подготовлен с учетом следующих предположений и ограничивающих условий:
Значения дополнительной регрессионной статистики для линейной зависимости в сравнительном подходе оценки недвижимости
Таблица 43 Значения дополнительной регрессионной статистики для степенной зависимости в сравнительном подходе оценки недвижимости
При анализе F-статистики определяется, является ли этот результат расчета (с высоким значение R2) случайным или нет. Если F-наблюдаемое больше, чем F-критическое, то взаимосвязь между переменными имеется. F-критическое можно получить из таблицы F-критических значений в справочнике по математической статистике. Для того чтобы найти это значение, используем односторонний тест, например, величину Альфа равную 0,05, а для числа степеней свободы (обозначаемых обычно v1 и v2), в нашем случае v1 = k = 3 и v2 = n - (k + 1) = 8 - (3 + 1) = 4, где k – это число переменных, а n – число точек данных. Из таблицы справочника F-критическое равно 6,59. F-наблюдаемое равно 25,72886281 при линейном тренде, 28,9936066 при степенном. И то и другое больше, чем F-критическое (6,59). Следовательно, полученные регрессионные уравнения подходят для предсказания оценочной стоимости недвижимости. И при линейной, и при степенной зависимости удовлетворяются требования принятия решений по статистическим показателям. В нашем случае целесообразнее взять за основу уравнение с большим значением R2 и F-статистикой. Этому условию удовлетворяет степенная зависимость. Ответ: цена 1 кв.м равна 49,637 тыс.руб. Использование корреляционно-регрессионного анализа при оценке недвижимости сравнительным подходомПри оценке недвижимости в рамках сравнительного подхода широко используются элементы корреляционно-регрессионного анализа. Корреляционно-регрессионный анализ как общее понятие включает измерение тесноты, направления связи и установление аналитического выражения (формы) связи (регрессионный анализ). Корреляционно-регрессионный анализ может быть представлен двумя методами: методом парной корреляции и методом множественной корреляции (многофакторный анализ). Для того чтобы провести корреляционно-регрессионный анализ, необходимо ознакомиться с основными терминами теории статистики. Термины приведены согласно [8]. Статистическая совокупность – множество однородных по качеству элементов (строений, помещений, площадей и объемов конкретного назначения), рассматриваемое как целое. Единица совокупности – единичный элемент, принадлежащий данному множеству. Генеральная совокупность – множество всех единиц совокупности с заданным определяющим признаком (множество однокомнатных квартир, множество домов со стенами из кирпича и т.д.). Число единиц генеральной совокупности определяется по результатам сплошного статистического обследования. Выборочная совокупность, выборка – подмножество нескольких (двух и более) единиц совокупности, входящих в генеральную совокупность. Случайная выборка – подмножество генеральной совокупности, единицы которого выбраны с соблюдением принципа случайности. Объем выборки (n) – число единиц генеральной совокупности, вошедших в выборку. Объем выборки, достаточный для оценки какого-либо признака с заданной точностью, определяется опытным путем или задается методикой оценки. Объем выборки, достаточный для взаимопогашения случайностей и получения статистических характеристик закономерного характера, равен 30. Выборка такого объема называется малой. Характер распределения значений признака в малых выборках приближается к нормальному с ростом числа испытаний. Минимальный объем выборки, позволяющий получить средние значения признака с указанием доверительных вероятностей, равен 5. Выборки такого объема называются сверхмалыми. Средняя величина – обобщающая характеристика совокупности фактов, полученная по результатам единичных испытаний. В средней величине проявляется действие закона больших чисел, ограничивающее случайности путем их взаимопогашения. Расчет средних величин В качестве среднего значения СВ могут использоваться различные величины, например, медиана, мода, среднее арифметическое выборки. Медиана ( Мода ( Среднее арифметическое Наиболее простой задачей, которую можно решать с
использованием данных о ценах на единичные объекты Х1,
Х2 … Xn, накопленных за определенный
промежуток времени, является определение средней цены объекта в выборке
где n – число накопленных значений цен (объем выборки). Размерность данного показателя – денежный эквивалент в целом, руб., долл. и т.п. Если использовать другую размерность – руб./кв. м или долл./кв. м, можно получить целую систему показателей среднего значения. Расчет величин разброса Средние величины характеризуют статистический ряд числом, но не отражают изменчивость наблюдавшихся значений признака, т. е. вариацию. Разброс (рассеяние) СВ может оцениваться различными величинами, например, размахом (диапазоном разброса), дисперсией или среднеквадратическим отклонением, доверительным интервалом, показателем вариации. Размах СВ
Дисперсия СВ ( Среднеквадратическое отклонение ( Среднеквадратическое отклонение генеральной совокупности обозначается греческой буквой ? «сигма», выборки – латинской s («эс»).
Доверительный интервал – это размах СВ, определенный не по всем ее значениям, а по заданной доле значений, примыкающих к среднему. Доверительный интервал строится влево и вправо по вычисленным показателям плюс/минус среднеквадратическое отклонение от среднего арифметического (среднеарифметическое в данном случае служит точкой отсчета и отложения доверительных интервалов). Доля значений, по которой определяется доверительный интервал, называется доверительной вероятностью. После расчетов необходимо посмотреть, сколько значений выборки попало в доверительный интервал плюс/минус три среднеквадратических отклонения (это соответствует разработанному в математической статистике «правилу трех сигм»). Обычно для правильно подобранной выборки доверительная вероятность равна 0,977. Таким образом, примерно 2% значений, попавших в выборку, являются «всплесками», т.е. «выскакивающими значениями». Их необходимо исключить из выборки и заново рассчитать указанные выше параметры выборки. Показатель вариации (
Рекомендуемое значение показателя вариации для жилых объектов
недвижимости при Парная корреляция5– связь между двумя признаками (результативным и факторным или двумя факторными). Парная корреляция подразумевает выявление наличия и формы корреляционной зависимости между результативным показателем (ценой) и одним из анализируемых факторных признаков (характеристикой). При этом предполагается условное равенство всех прочих характеристик в сравниваемых объектах, а результативный показатель есть функция от значения анализируемой ценообразующей характеристики аналогичных объектов:
По общему направлению корреляционная связь может быть прямой или обратной. При прямой связи увеличение факторного признака приводит к повышению результативного, и наоборот, если при повышении факторного признака результативный уменьшается, это говорит о наличии обратной связи. Одним из главных статистических показателей, знак при котором указывает направление корреляционной связи, является коэффициент корреляции (знак «+» говорит о наличии прямой связи, «-» – об обратной). Коэффициент корреляции является мерой тесноты связи между ценой и анализируемой характеристикой. Например, для определения тесноты парной линейной зависимости применяется линейный коэффициент корреляции (r). Линейный коэффициент корреляции рассчитывается следующим образом:
Линейный коэффициент корреляции изменяется в пределах от -1 до +1. Чем ближе его значение по модулю к 1, тем теснее связь. В силу того, что сравниваемые объекты имеют, как правило, несколько ценообразующих характеристик, линейный коэффициент корреляции может использоваться для выделения какой-либо одной из них, оказывающей максимальное влияние на формирование цен выбранных объектов-аналогов. Кроме коэффициента корреляции в корреляционно-регрессионном анализе используются и другие статистические показатели: среднеквадратическое отклонение, среднеквадратичная ошибка, коэффициент вариации, достоверность и пр. Одним из важных этапов корреляционно-регрессионного анализа является выбор уравнения регрессии. Выбор уравнения регрессии, с помощью которого производится расчет стоимости оцениваемого объекта, осуществляется на основе значений коэффициента корреляции и (или) достоверности каждого анализируемого вида регрессионного уравнения. При этом могут быть использованы следующие основные виды корреляционной зависимости (уравнений регрессии):
Оценка меры достоверности анализируемого уравнения регрессии Мера достоверности (D) анализируемого уравнения
регрессии оценивается с помощью процентного соотношения среднеквадратической
ошибки уравнения (Se) и математического ожидания по результативному
признаку (
Среднеквадратическая ошибка находится по формуле
где
i– число параметров уравнения регрессии В случае, если максимальное значение D не превышает 15%, анализируемое уравнение регрессии достаточно корректно отображает корреляционную связь и может быть использовано для расчета стоимости оцениваемой недвижимости. Многофакторный анализ предполагает выявление наличия и формы корреляционной зависимости между результативным показателем и несколькими факторными признаками (параметрами):
Применение факторного анализа для расчета стоимости оцениваемого объекта дает более точные результаты по сравнению с парной корреляцией и поэтому в большинстве случаев является более приоритетным. К тому же метод парной корреляции в оценке недвижимости применим в основном для расчета отдельных поправок, а метод множественной корреляции позволяет рассчитать стоимость оцениваемой недвижимости в целом. Например, может быть использована линейная регрессия вида
Рассмотрим применение однофакторного корреляционно-регрессионного анализа для расчета стоимости недвижимости методом парной корреляции на следующем примере. Следует сказать, что на практике однофакторные модели взаимосвязи встречаются редко, т.к. в большинстве случаев стоимость недвижимости зависит от нескольких переменных. Применение однофакторной модели допустимо при условии схожести всех остальных характеристик. Объект оценки – офис общей площадью 160 кв.м. Имеется информация об объектах-аналогах в отношении их общей площади и цены продажи. Таблица 31 Линейный метод или метод средних в финансовой математикеОдним из простейших и наиболее популярных методов установления суммы обесценивания является метод средних, обычно называемый линейным методом. В этом методе предполагается, что сумма обесценивания для каждого года является одинаковой (постоянной). Таким образом, если C равно первоначальной стоимости иS является стоимостью остатков, или коммерческой стоимостью, в конце периода использования изn лет, тогда годовое обесценивание принимается равным (C - S)/n . Этот метод проиллюстрируем следующим примером. ПРИМЕР Машина стоила компании 33 млн рб. Оценено, что полезная жизнь машины будет 5 лет и что стоимость остатков будет 3 млн рб. Найти годовое обесценивание при помощи линейного метода и построить расписание, которое показывает для каждого года годовое обесценивание, книжную цену машины и полное обесценивание. 140
Следует заметить, что имеется два главных возражения линейному
быстрее в течение первых лет, так что книжные цены в течение этих лет значительно выше, чем реальные рыночные цены. Следовательно,
используется Расчетные значения цены 1 кв.м недвижимости по различным функциям корреляционно-регрессионного анализа
На основе расчетных данных проведем сравнение уравнений по коэффициенту корреляции, коэффициенту детерминированности среднеквадратической ошибки и достоверности. Таблица 36 Расчетные значения цены 1 кв.м по различным функциям в сравнительном подходе оценки недвижимости
На основе расчетных данных проведем сравнение уравнений по коэффициенту корреляции, коэффициенту детерминированности среднеквадратической ошибки и достоверности. Таблица 36 Статистические показатели в сравнительном подходе оценки недвижимости
По результатам анализа табл. 33 выборку можно признать однородной. Выберем линейное уравнение регрессии Из табл.34 возьмем коэффициенты уравнения. В итоге линейное изменение цены в зависимости от площади можно описать следующим уравнением:
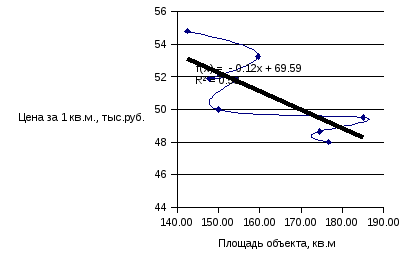
Дополнительную информацию по стандартным функциям Microsoft Excelможно получить в справке по каждой функции. Вид уравнения также можно определить по графику, который строится по заданным и известным значениям с помощью точечных диаграмм в редакторе MicrosoftExcel.
Рис.3. Линейная зависимость между площадью и стоимость 1 кв.м Выберем степенное уравнение регрессии
Выберем логарифмическое уравнение регрессии
Выберем экспоненциальное уравнение регрессии
Выберем полиномиальное (второго уровня) уравнение регрессии
На основании уравнений рассчитаем новые значения стоимости 1 кв.м. Таблица 35 Статистические показатели моделей оценки стоимости недвижимости
По результатам анализа табл. 33 выборку можно признать однородной. Выберем линейное уравнение регрессии Из табл.34 возьмем коэффициенты уравнения. В итоге линейное изменение цены в зависимости от площади можно описать следующим уравнением:
Дополнительную информацию по стандартным функциям Microsoft Excelможно получить в справке по каждой функции. Вид уравнения также можно определить по графику, который строится по заданным и известным значениям с помощью точечных диаграмм в редакторе MicrosoftExcel.
Рис.3. Линейная зависимость между площадью и стоимость 1 кв.м Выберем степенное уравнение регрессии
Выберем логарифмическое уравнение регрессии
Выберем экспоненциальное уравнение регрессии
Выберем полиномиальное (второго уровня) уравнение регрессии
На основании уравнений рассчитаем новые значения стоимости 1 кв.м. Таблица 35 Список литературы и источников на тему "Регрессионная статистика в оценке стоимости"
Другие похожие работы |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
© 2002 - 2024 RefMag.ru |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
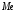 )
– это одно из значений СВ в выборке, относительно которого половина значений
превышает медиану, а другая половина не превышает (для расчета медианы выборку
следует проранжировать, т.е. выстроить в числовом порядке от большего к
меньшему или наоборот).
)
– это одно из значений СВ в выборке, относительно которого половина значений
превышает медиану, а другая половина не превышает (для расчета медианы выборку
следует проранжировать, т.е. выстроить в числовом порядке от большего к
меньшему или наоборот).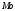 )
– это наиболее часто встречающееся значение в выборке.
)
– это наиболее часто встречающееся значение в выборке.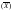 –
это расчетная величина, определяемая по формуле (34).
–
это расчетная величина, определяемая по формуле (34).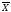 .
.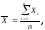
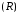 –
это разность между максимальным и минимальным ее значением:
–
это разность между максимальным и минимальным ее значением:
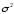 или
или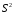 )
– расчетная величина, определяемая по формулам (36) или (38) и характеризующая
степень отклонения каждого из значений СВ от среднего в квадрате.
)
– расчетная величина, определяемая по формулам (36) или (38) и характеризующая
степень отклонения каждого из значений СВ от среднего в квадрате.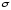 или
или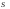 ,
иначе стандартное отклонение) – расчетная величина, определяемая по формулам
(37) или (39) и характеризующая степень отклонения каждого из значений СВ от
среднего.
,
иначе стандартное отклонение) – расчетная величина, определяемая по формулам
(37) или (39) и характеризующая степень отклонения каждого из значений СВ от
среднего.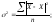
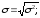
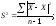
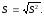
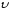 )
– расчетная величина, определяемая по формулам (40) или (41) (в зависимости от
того, что анализируется – генеральная совокупность или выборка) и
характеризующая степень отклонения каждого из значений СВ от среднего в
процентах.
)
– расчетная величина, определяемая по формулам (40) или (41) (в зависимости от
того, что анализируется – генеральная совокупность или выборка) и
характеризующая степень отклонения каждого из значений СВ от среднего в
процентах.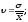
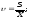
 развитом
рынке жилищной недвижимости 10% [34].
развитом
рынке жилищной недвижимости 10% [34].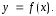
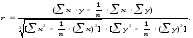
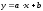 ;
;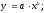
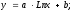
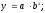
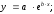
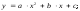
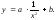
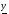 ):
):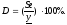
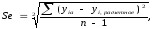
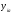 –
фактическое значение ценыi– го объекта-аналога;
–
фактическое значение ценыi– го объекта-аналога; –расчетное
значение цены i– го объекта-аналога по выбранному уравнению
регрессии;
–расчетное
значение цены i– го объекта-аналога по выбранному уравнению
регрессии; –количество
объектов в выборке;
–количество
объектов в выборке; .
.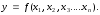
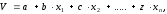
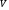 –стоимость
объекта оценки;
–стоимость
объекта оценки;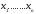 –основные
ценообразующие характеристики сравниваемых объектов;
–основные
ценообразующие характеристики сравниваемых объектов;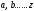 –коэффициенты
регрессии.
–коэффициенты
регрессии.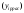
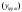
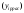
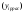
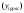
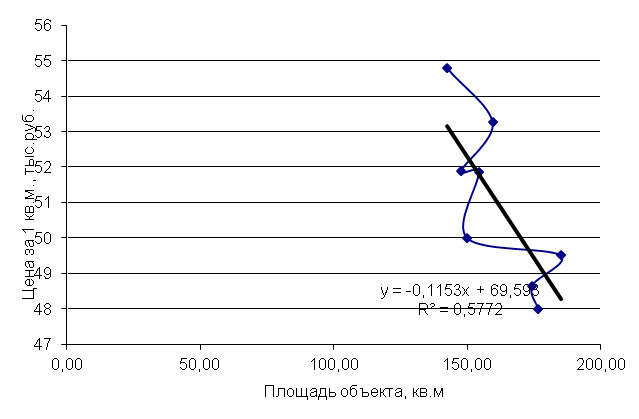
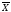 ),
тыс.руб.
),
тыс.руб.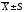 )
)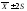 )
)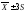 )
)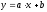 и
найдем коэффициенты. Для этого введем значения в КнигуMicrosoftExcel, в меню
СЕРВИС выберем функцию АНАЛИЗ ДАННЫХ, из предлагаемых наименований выберем
РЕГРЕССИЯ, после чего появится окно, в которое следует внести значения
и
найдем коэффициенты. Для этого введем значения в КнигуMicrosoftExcel, в меню
СЕРВИС выберем функцию АНАЛИЗ ДАННЫХ, из предлагаемых наименований выберем
РЕГРЕССИЯ, после чего появится окно, в которое следует внести значения (цены)
и
(цены)
и (площади
объекта оценки). После внесения данных появится таблица 34 (см. с. 102).
(площади
объекта оценки). После внесения данных появится таблица 34 (см. с. 102).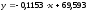 ;
;
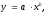 аналогичное
линейному:
аналогичное
линейному: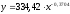 ;
;
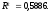
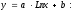
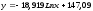 ;
;
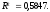
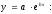
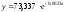 ;
;
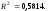
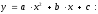
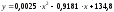 ;
;