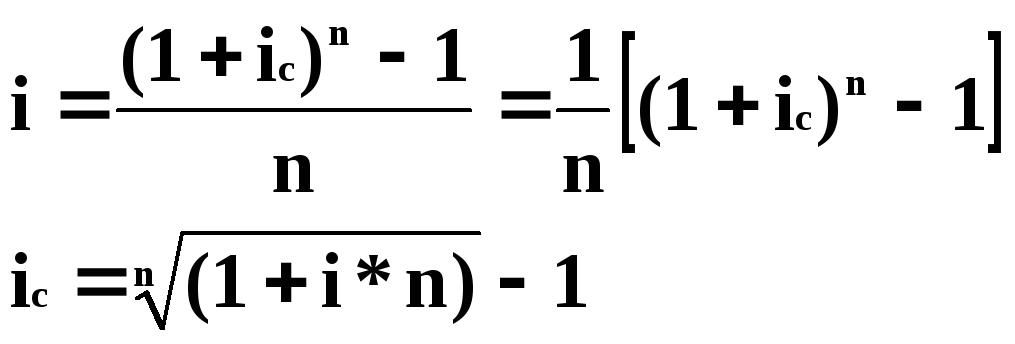|
|
Примеры: | контрольные | курсовые | дипломные | отзывы |
|
Процентная ставка в оценке стоимостиВнутригодовые процентные начисления в финансовой математикеВ случае, если начисление процентов производится несколько раз в год, то:
где r - годовая ставка процента; m - количество начислений в году; n - количество лет. Пример 7. В банк помещена сумма 5 млн. руб. на два года под 20 % годовых. Определить накопленную сумму при условии, что накопление процентов производится: а) 1 раз в год; б) 2 раза в год; в) 4 раза в год; г) ежемесячно. а) б) в) г) Выводы.
Определение процентной ставки в финансовой математикеКогда неизвестна процентная ставка i , но заданыR ,n иA ( илиS ) , мы вновь обращаемся к формуле(3) A = R a п i
=R (1 - (1 +i) которая может рассматриваться как уравнение относительно процентной ставки i . Оно может быть преобразовано к виду (A/R)(1 +i)п+1 - (1 +A/R)(1 +i)п + 1 = 0 Такое уравнение относится к классу нелинейных алгебраических уравнений и его решение в общем случае не выражается в явной аналитической форме, так что его решение может быть осуществлено только численными методами. Вместе с тем, используя метод линейной интерполяции, можно достаточно просто находить приближенные решения этого уравнения. Продемонстрируем это на примерах. ПРИМЕР 1 Петров вкладывал в сберегательный банк по 25 тыс рб в конце каждого месяца в течение 5 лет. В настоящее время у него на счете накопилось 1625 тыс рб. С какой номинальной нормой процента дляm = 12 начисляет проценты сберегательный банк ?
61  На основе таблицы для функции составных платежей s п i составим следующую табличку
Составляем пропорцию линейной интерполяции j12 0,03 65,00000 64,64671 0,35329 0,035 0,03 65,46671 64,64671 0,81940. Откуда получаем j12 = 0.03216 . ПРИМЕР 2 Фирма продает товар стоимостью 100 млн рб по следующему платежному расписанию : 10 млн рб сразу и 10 ежемесячных взносов по 9&55 млн рб каждый, первый взнос делается через три месяца. Какую номинальную норму дляm = 12 предусматривает такое расписание ? РЕШЕНИЕ 10 ежемесячных платежей образуют отсроченный аннуитет с текущей стоимостью 90 млн рб на день покупки как показано на временной диаграмме
9.55 9.55 ... 9.55 9.55 90 Уравнение аннуитета имеет вид
Вновь обращаясь к таблицам функций составных платежей, составляем вспомогательную табличку
62 Пропорция линейной интерполяции имеет вид
представлять точность этих приближений. Приведем некоторые данные, касающиеся ошибок при определении нормы процента с использованием
Ошибка зависит сильнее от разности между двумя соседними значениями нормы процента в таблице и гораздо слабее - от величины n . Анализ ошибок для всех значений параметров таблиц показывает, что ошибка редко превосходит величину (n/10)( разность норм процента )2 . Эта величина для расчета i в примере 1 равна (60/10)( 0,07/24 - 0,01/4 ) = 0,00000104 . и для j12 составляет 0,0000125 . Для примера 2 расчетj12 с точностью до шестого знака дает 0,095719 . Определение процентной ставки для общего аннуитета в финансовой математикеПростейший способ определения нормы процента для общего аннуитета состоит в определении нормы процента для простого аннуитета на интервал платежа, а затем преобразовании этой нормы в эквивалентную норму на требуемый период начисления процентов. При этом в отсутствии вычислительных средств снова можно для получения приближенного решения воспользоваться методом линейной интерполяции и таблицами функций составных платежей. ПРИМЕР Обыкновенный аннуитет на 750 тыс рб поквартально на 7 лет может быть куплен за 15750 тыс рб. Какая номинальная норма, конвертируемая ежемесячно, использована для реализации инвестиции покупателя ? РЕШЕНИЕ Сначала решим задачу простого аннуитета : какой должна быть поквартальная нормаi начисления процентов ? Для этой вспомогательной задачи используем равенство 750 а2 8
i = 15750 илиа2 8 i = (1 - (1 +i) Если под рукой нет вычислительных средств для численного решения этого уравнения, воспользуемся интерполяцией при помощи таблиц. Составим следующую вспомогательную табличку (для рассматриваемого 72
что дает i = 0,02104 илиi = 2,1 % . Однако нам нужно определить неi , аj12 , которая должна быть связана сi соотношением эквивалентности ( 1 + j12 / 12 )12 = ( 1 +i )4 . Разрешая его относительно j12 получим j12 = 12 ((1 +i )1/3 - 1) .
приведенной выше вспомогательной табличкой, составляя новую пропорцию линейной интерполяции
ПРИМЕР 2 Решить предыдущий пример, если норма процента конвертируется по полугодиям. РЕШЕНИЕ Процесс решения точно такой же, как и в предыдущем случае, только вместоj12 необходимо использоватьj2 , так что соотношение эквивалентности принимает вид 73 Определение реальной процентной ставки с учетом инфляции в финансовой математикеВведем показатели, характеризующие реальную доходность кредитных операций в условиях инфляции. Пусть срок действия ссуды равен T; S0- начальная сумма; ST – наращенная сумма денег, измеренная по номиналу. Для операции наращения суммы по простой процентной ставке i на интервале времени Т в качестве показателя реальной доходности возьмем простую процентную ставку iэ, обеспечивающую рост начальной суммы S0 за тот же срок Т до реального значения наращенной суммы С: С = S0 •(1 + iэ·Т) . Отсюда находим:
где С вычисляется по формуле (33). Если реальное значение наращенной суммы С оказывается меньше начальной суммы S0 (то есть, операция убыточна), то показатель доходности ссудной операции i, является отрицательным. Аналогично, для операции наращения суммы по сложной процентной ставке i в качестве показателя реальной доходности на интервале времени Т возьмем сложную процентную ставку iэ, обеспечивающую рост начальной суммы S0 за тот же срок T до реального значения наращенной суммы С: С = S0 • (1+ iэ)T. В частном случае, когда h — темп инфляции за период начисления, а срок ссуды Т равен целому числу n периодов начисления, и для вычисления С используется формула (36), находим явное выражение для iэ:
И в этом случае показатель реальной доходности операции может быть отрицательным, если темп инфляции за период начисления превышает объявленную процентную ставку. Переменные ставки сложных процентов в финансовой математикеЕсли ссуда долгосрочная, то в течение срока ее действия ставки процента могут изменяться. Пусть общий срок ссуды Т разбивается на части T1, Т2,...Tn причем в течение срока Т1 применяется процентная ставка i1; в течение срока T2 применяется процентная ставка i2; …………………………………………………………… в течение срока Тn применяется процентная ставка in. Обозначим множитель наращения за срок Тk через Аk, а наращенную к концу срока Tk сумму через Ak. Пусть расчет ведется по общему методу, тогда Ak = (1+ik)Tk . По формуле (11) находим:
В краткой форме полученная формула записывается так:
Попутно мы показали, что коэффициент наращения А за весь срок ссуды равен произведению коэффициентов наращения на составляющих его интервалах: A=A1A2A3…An (15) Этот результат носит название принципа стабильности рынка. Пояснения к заданиям по финансовой математикеПростые проценты. Сущность метода начисления простых процентов по простым процентам в том, что проценты начисляются в течение всего срока на одну и ту же величину капитала, представляемого в кредит. Наращенная сумма – это совокупная величина основного долга и процентных денег за весь кредитный период или это сумма накопленного заемщиком долга. Сложные проценты. Сущность метода начисления по сложным процентам в том, что база для начисления процентов от одного расчетного периода к другому. Сумма начисленных в каждом периоде процентов добавляется к капиталу предыдущего периода, а начисление процентов в последующем периоде производится на эту, уже наращенную величину первоначального капитала. Механизм наращения первоначальной суммы (капитала) по сложным процентам называется капитализацией. Дисконтирование. Дисконтирование – приведение экономических показателей (выручки, затрат, капитала) будущих лет к сегодняшней ценности. В качестве ставки дисконтирования может служить ставка банковского процента, учетная ставка, темп инфляции или другой показатель. Учет инфляции в расчетах. Инфляция – процесс снижения покупательной способности под воздействием определенных факторов. Влияние инфляции на величину экономических показателей определяется с помощью индекса инфляции. Финансовые ренты (аннуитеты). Современные финансово-банковские операции часто предполагают не отдельные или разовые платежи, а некоторую их последовательность во времени. Такая последовательность платежей называется потоком платежей, а отдельные элементы этого ряда – члены потока. Поток платежей, все члены которого положительные величины, называется финансовой ренты или аннуитетом, независимо от назначения или происхождения платежей. Рента характеризуется параметрами:
По моменту выплат платежей в пределах периода финансовые ренты подразделяются на :
Планирование погашения долга. Расходы, связанные с погашением кредита, т.е. погашением основного долга и выплатой процентов по нему, называется расходами по обслуживанию долга или амортизацией кредита. Существуют различные способы погашения задолженности. Участники кредитной сделки оговаривают их при заключении контракта. В соответствии с контрактом составляется план погашения долга. Эквивалентность процентных ставок. Процентные и учетные ставки решают одинаковые задачи: определение степени доходности при операции наращения или размеры дисконтированных сумм при учетной операции. В связи с этим возможен выбор таких процентных ставок, при пользовании которых финансовые последствия окажутся равноценными. Процентные ставки и методы их начисления в финансовой математикеПростые и сложные проценты. Стандартным временным интервалом в финансовых операциях является один год. Поэтому наиболее распространен вариант, когда процентная ставка устанавливается в виде годовой ставки, подразумевающей однократное начисление процентов по истечение года. Известны две основные схемы дисконтированного начисления процентов:
Схема простых процентов предполагает неизменность базы, с которой происходит начисление.
Схема сложных процентов предполагает, что очередной годовой доход исчесляется не с исходной величины инвестированного капитала, а с общей суммы, включающей также и ранее начисленные, и невостребованные инвестором проценты.
Очень важно помнить, что - при 0 < n< 1 - при n = 1 - при n> 1 Таким образом, в случае ежегодного начисления процентов, для лица, предоставляющего кредит:
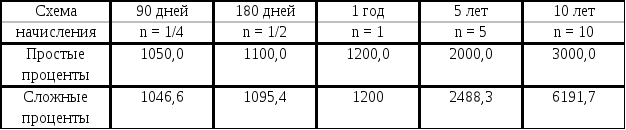
Пример 1. Рассчитать наращенную сумму с исходной суммы 1000$ при размещении ее в банке на условиях начисления простых и сложных процентов, если годовая ставка 20 %, период наращивания: 90 дн., 180 дн., 1 год, 5 лет, 10 лет. ($)
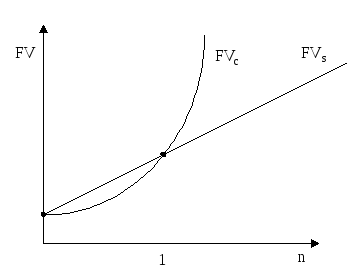
Рис. 2. Простая и сложная схема наращивания капитала. Пример2. Компания хочет купить машину для снятия фотокопий за 10 000$. Продавец согласен, чтобы компания выплатила деньги по истечение 2 лет, при условии, что она заплатит за это 14 простых процентов за каждый год. Определить сумму процентов и полную выплату. Проценты:
Если продавец машины согласен на отсрочку платежа всего на 90 дней, тогда
Если продавец машины согласен на отсрочку платежа на 15 месяцев, тогда
Процедура начисления процентов на проценты (сложные проценты) называются компаундингом. Множитель Пример 3. Вклад 3000$ помещены в банк под 5 % годовых на 3 года. Какая сумма будет накоплена через 3 года (сложные %)?
Пример 4. Предприниматель желает инвестировать значительную сумму денег в акции некоторой корпорации. Корпорация выплачивает ежегодно дивиденды на одну акцию в сумме 3 %. Ожидается, что в течение ближайших 3 лет дивиденды будут увеличиваться ежегодно на 20 %. Рассчитать величину дивидендов для каждого года.
В практических расчетах при реализации схемы сложных процентов для быстрой оценки эффективности предлагаемой процентной ставки пользуются приблизительным расчетом времени, необходимого для удвоения инвестированной суммы. Это правило называется «правило 72-х» и заключается в следующем: если r-процентная ставка, выраженная в процентах, то k = 72/r представляет собой число периодов, за которое исходная сумма приблизительно удваивается. Если базовым периодом, т. е. периодом наращивания является год, то в расчете используется годовая ставка, если квартал, то необходимо использовать квартальную ставку. Это правило хорошо срабатывает для небольших значений r (до 20 %).
Проценты в финансовой математикеВсякий собственник, имеющий квартиру или гараж, которые он не использует, может сдать их в наем, получая за это определенную плату. Точно также человек, имеющий деньги, которые он не использует, может их дать взаймы другому лицу (или, используя более общий термин, - инвестировать) за определенное вознаграждение. Доход от инвестированного капитала или, в более узком смысле, вознаграждение за использование денег, называется процентными деньгами или краткопроцентами. Сумма денег, данных взаймы, называетсяосновной иликапиталом. Обычно заем дается на определенное время -период. Сумма процентных и основных денег, полагающаяся в конце периода, называетсяитогом. В общем случае отношение процента за период к основной сумме (капиталу) называетсянормой процента. Эта норма чаще всего выражается в форме процентов, при расчетах используются эквивалентные десятичные (реже - натуральные) дроби. При заключении конкретных сделок для обозначения нормы процентов обычно используется другое название -процентная ставка. ПРИМЕР Иванов взял в сберегательном банке ссуду 10000 рб. Если банк начисляет 250 рб процентных денег за использование этой суммы в течение 6 месяцев, какой будет норма процента за этот период ? РЕШЕНИЕ Обозначим норму процента за шести месячный период черезi. Тогдаi = 250/10000 = 0.025 = 2.5%. Проценты за дробное число летВ различных сделках срок не всегда есть целое число лет, он может быть равен и дробному числу лет. Пусть t = a+ b, где t – период сделки в годах, a – целая часть t. b – дробная часть t. В таких случаях проценты могут начисляться двумя способами:
Заметим, что если общий срок менее года, наращенная сумма
вычисляемая по смешанному методу больше, чем наращенная сумма вычисляемая по
формуле сложных процентов, т.к. Задача № 7.1. Клиент банка вносит депозит $3000 на 3,5 года под 40% годовых. Определить величину депозита в конце периода используя два метода: по формуле сложных процентов и на основе смешанного метода. Решение. По формуле сложных процентов На основе смешанного метода: Ответ: $9740 и $9879,4. Задача № 7.2. Размер депозита 10 млн.руб. Номинальная годовая ставка 50%. Проценты начисляются по полугодиям. Найти наращенную сумму по смешанному методу, если срок депозита 27 месяцев. Решение. Используя смешанный метод, находим:
Ответ: наращенная сумма 25939941 руб. Расчет процентной ставки в финансовой математике:- при наращении по сложной годовой ставке %, - при наращении по номинальной ставке % m раз в году, - при наращении по постоянной силе роста. Ставка дохода на собственный капитал в оценке недвижимостиСтавка дохода на собственный капитал – расчитывается как отношение ежегодных денежных поступлений после вычета расходов по обслуживанию кредита и до уплаты налогов к размеру собственного капитала инвестора в объекте недвижимости. С учетом других факторов, позволяет проводить оценку привлекательность инвестиций в объекты недвижимости за счет собственных средств.
 Учетные ставки в финансовой математикеЗа вексель, учтенный за 5 лет по простой учетной ставке (4+ав) процентов, заплачено 4 млн.руб. Определите номинальную величину векселя. Эквивалентность простой и сложной ставок в финансовой математике
По простой Эквивалентность ставок в финансовой математикеБанк принимает вклады до востребования под сложную процентную ставку (10+а)% годовых при временной базе 365 дней. Какую простую годовую учетную ставку должен применить банк при учете векселя за 250 дней до срока его погашения, чтобы обеспечить себе такую же доходность , как и по вкладам до востребования? При расчете используется временная база 360 дней. 9. Инфляция и начисление сложных и непрерывных процентов . На вклад (30+а) тыс.руб. ежеквартально начисляются сложные проценты по номинальной годовой процентной ставке (10+а)%. Оцените сумму вклада через 21 месяц с точки зрения покупательной способности, если ожидаемый темп инфляции1% в месяц, Какова должна быть величина номинальной положительной процентной ставки? Как изменится ситуация, если темп инфляции будет 2% в месяц? Эквивалентные ставки и их использование в финансовой математике
Эффективная годовая ставка процента в финансовой математикеДано: – исходная сумма PV;
Этому набору исходных величин в рамках одного года соответствует определенное значение наращенной величины FV. Найти: такую годовую ставку То есть схемы {PV, FV, r, m>1} и {PV, FV,
Эффективная ставка зависит от количества внутригодовых начислений, причем с ростом m она увеличивается. При непрерывном начислении процентов
Пример 12. (д. з.) Предприниматель может получить ссуду на следующих условиях:
Какой вариант следует выбрать? а) б) Вариант б) является более предпочтительным для предпринимателя. Пример 13. Вычислить эффективную годовую ставку процента по займу корпорации, если номинальная ставка 12 % годовых и проценты начисляются: а) поквартально; б) 2 раза в год; в) ежемесячно; г) непрерывно. а) б) в) г) Эффективная процентная ставка в финансовой математикеДля сравнения реального относительного дохода за год при начислении процентов один иm раз, введем понятие эффективной ставки процентов. Эффективная годовая ставка процентов iэф - это ставка, измеряющая реальный относительный доход, который получают в целом за год от начисления процентов, т. е. iэф - это годовая ставка сложных процентов, которая дает тот же результат, что и m - разовое начисление процентов по ставке за период i = j/ m . Эффективная ставка находится из условия равенства двух соответствующих коэффициентов наращения за один год: 1 + iэф = ( 1+ j / m ) m. Отсюда следует, что iэф = ( 1+ j / m ) m - 1(11) Пример. Определите эффективную ставку сложных процентов с тем, чтобы получить такую же наращенную сумму, как и при использовании номинальной ставки j=18 %, при ежеквартальном начислении процентов (m=4). Решение. Из формулы (11) получаем: iэф = ( 1 + 0,18 / 4 )4 - 1 = 0, 1925 ( или 19, 25 %). Пример. Найдите эффективную ставку, если номинальная ставка равна 25 % при ежемесячном начислении процентов. Решение. iэф = ( 1 + 0,25 / 12 )12 - 1 = 0,2807 или 28,07 %. Для сторон в сделке безразлично, применить ставку 25 % (при помесячном начислении) или годовую ставку 28,07 %. Пример. Найдите номинальную процентную ставку, проценты по которой начисляются по полугодиям, эквивалентную номинальной ставке 24% с ежемесячным начислением процентов. Решение. Пусть j2 - процентная ставка, соответствующая начислению по полугодиям, j12 - по месяцам. Из равенства коэффициентов наращения получаем: ( 1 + j2 / 2 )2 = ( 1 + j12 / 12 )12, отсюда 1 + j2 / 2 = ( 1 + j12 / 12 )6 ? j2 = 2[( 1 + j2 / 12 )6 - 1] = = 2 [( 1 + 0,24/12)6 - 1 ] = 0,25 или j2= 25 %. Список литературы и источников на тему "Процентная ставка в оценке стоимости"
Другие похожие работы |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
© 2002 - 2024 RefMag.ru |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|

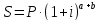
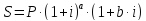
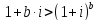 для b<1.
для b<1.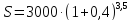 =9740.
=9740.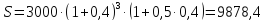 .
.