|
|
Примеры: | контрольные | курсовые | дипломные | отзывы |
|
Практикум по оценочной деятельностиПрактикум по финансовой математикеПО ФИНАНСОВОЙ МАТЕМАТИКЕ (автор Галиаскаров Ф.М.) 2012 г. Глава 1. Основные формулы, применяемые в финансовых расчетах 1.1. Простые и сложные проценты Под процентной ставкойпонимается относительная величина дохода за фиксированный отрезок времени. Процентыразличаются по базе их начисления. Применяется постоянная или последовательно изменяющаяся база для расчета. В последнем случае за базу применяется сумма, полученная на предыдущем этапе наращения или дисконтирования, т.е. проценты начисляются на проценты. При постоянной базе используютпростые, при измененной -сложные процентные ставки. Под наращенной суммойссуды (долга, депозита, других видов выданных в долг или инвестированных денег) понимают первоначальную ее сумму с начисленными процентами к концу срока. Наращение по простой процентной ставке:
где S – наращенная сумма; P – первоначальная сумма, n – срок, r– ставка наращения (десятичная дробь). Наращение по сложной процентной ставке:
где j- сложная процентная ставка; n - число лет наращения,m– число начислений процентов в году. Номинальная ставка– это годовая ставка сложных процентов при одноразовом начислении процентов в году по ставкеj. Эффективная ставка– это годовая ставка сложных
процентов, которая дает тот же результат, что и m-разовое начисление процентов в
году по ставке Наращение по непрерывной процентной ставке: При непрерывном наращении процентов применяют особый вид
процентной ставки - силу роста (
Дисконтирование и учет по простым процентным ставкам. Термин дисконтированиеупотребляется как средство определения любой стоимостной величины, относящейся к будущему, на некоторый, более ранний момент времени. В финансовой практике часто сталкиваются с задачей, обратной наращению процентов: по заданной сумме S, которую следует уплатить через некоторое время n , необходимо определить сумму полученной ссуды P. Такая ситуация может возникнуть, например при разработке условий контракта. Расчет P по S необходим и тогда, когда проценты с суммы S удерживаются вперед, т.е. непосредственно при выдаче ссуды. В этом случае говорят, что сумма S дисконтируетсяилиучитывается, сам процесс начисления процентов и их удержание называетсяучетом, а удержанные проценты -дисконтом В зависимости от вида процентной ставки применяют два метода дисконтирования - математическое дисконтированиеибанковский (коммерческий) учет. В первом случае используется ставка наращения, во втором - учетная ставка. Математическое дисконтирование представляет собой формальное решение задачи, обратной наращению первоначальной суммы ссуды.
Банк или иное финансовое учреждение до наступления срока платежа по векселю или иному платежному обязательству приобретает его у владельца по цене, которая меньше суммы, указанной на векселе, т.е. покупает (учитывает) его с дисконтом (т.е. со скидкой). Получив при наступлении срока векселя деньги, банк реализует дисконт. При учете векселя применяется банковский или коммерческий учет, согласно этому методу проценты за пользование ссудой в виде дисконта начисляются на сумму, подлежащую уплате в конце срока. При этом применяется учетная ставка d.
Для ставки наращения прямой задачей является определение наращенной суммы, обратной – дисконтирование. Для учетной ставки, наоборот, прямая задача заключается в дисконтировании, обратная – в наращении . Ставка Прямая задача Обратная задача r d Учетная ставка отражает фактор времени более жестко. Например, при d = 20 % уже 5-ти летний срок достаточен для того, чтобы владелец векселя ничего не получил при его учете. Определение срока ссуды и величины простой процентной ставки Продолжительность срока ссуды в годах получим, решив уравнения (1) и (5) относительно n:
По этим же уравнениям можно определить и процентные ставки:
Определение срока платежа и сложных процентных ставок. Продолжительность срока платежа в годах получим, решив уравнения (2) относительно n:
Поэтому же уравнению можно определить и сложную процентную ставку:
Продолжительность срока платежа в годах при наращении по
постоянной силе роста
Поэтому же уравнению можно определить и силе роста
Раздел 1
ПРАКТИЧЕСКИЕ ЗАДАНИЯ ДЛЯ ЗАКРЕПЛЕНИЯ МАТЕРИАЛА Задание 1. Оценка денежных потоков от использования недвижимости во времени
3. Мария Ивановна сдала свою вторую квартиру в аренду, что позволит ей получать в течении 5 лет по окончании каждого года 100 000 руб. На протяжении последующих 10 лет ежегодные арендные платежи составят уже 150 000 руб., также вносимые в конце каждого года. Мария Ивановна через 15 лет планирует продать эту квартиру за 1 900 000 руб. За сколько должна была бы продать свою собственность Мария Ивановна сегодня, если бы она рассчитывала получить 10 %-ый доход, накапливаемый ежегодно? 4. Какую сумму получил продавец 3-х - комнатной квартиры от покупателя и положил на депозитный счет на пять лет под 10% годовых, если известно, что раз в году он снимал со счета 600 тыс. руб? 5. Компания планирует через 6 лет полностью заменить свой автопарк. Для этого она ежегодно переводит на счет в банке по 600 000 руб. Банк начисляет по вкладам 12% годовых. Определить, какой суммой будет располагать компания на замену автопарка. 6. Предоставление склада в аренду в течение 4 лет обеспечит доход 24 млн.руб. в год. В конце четвертого года он будет продан за 300 млн.руб. Рассчитайте текущую стоимость доходов, если ставка дисконта для дохода от аренды составляет 9 %, а для продажи – 15%. 7. Какую сумму в течение 10 лет необходимо в конце года откладывать под 20 % годовых, чтобы купить дачу за 1500 тыс. руб.? 8. При покупке дома стоимостью 50 000 $ предоставлена рассрочка на 9 лет. Определить ежегодные платежи при ставке 10%. 9. Владельцы кондоминиума планируют заменить кровлю на всех своих зданиях через 10 лет. Они полагают, что через 10 лет им это обойдется в 150 000 руб. Какую сумму они должны депонировать в конце каждого года с учетом того, что средства на счете будут накапливаться по годовой ставке 10 %? 10. Господин Смит приобрел место для парковки автомобиля за 18 000 $. Он считает, что сможет сдать его в аренду за 2 000 $ чистой годовой ренты, выплачиваемой в конце каждого из последующих 10 лет. Он также полагает, что в конце 10-го года собственность может быть продана за 40 000 $. При ставке 15% определить: Выгодна ли оказалась данная покупка для господина Смита и насколько? Список литературы и источников на тему "Практикум по оценочной деятельности"
Другие похожие работы |
||
|
|
||
|
© 2002 - 2024 RefMag.ru |
||
|
|
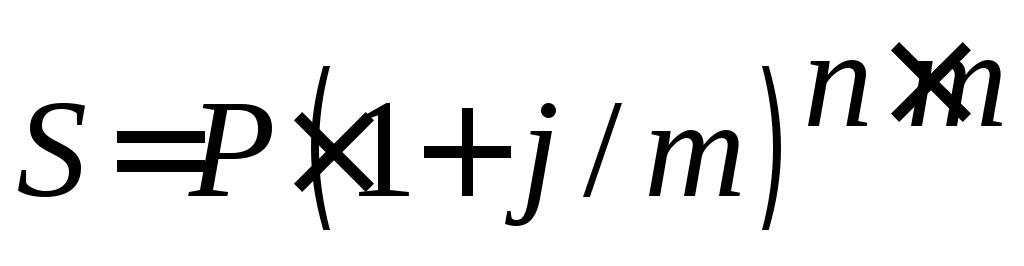 , (2)
, (2)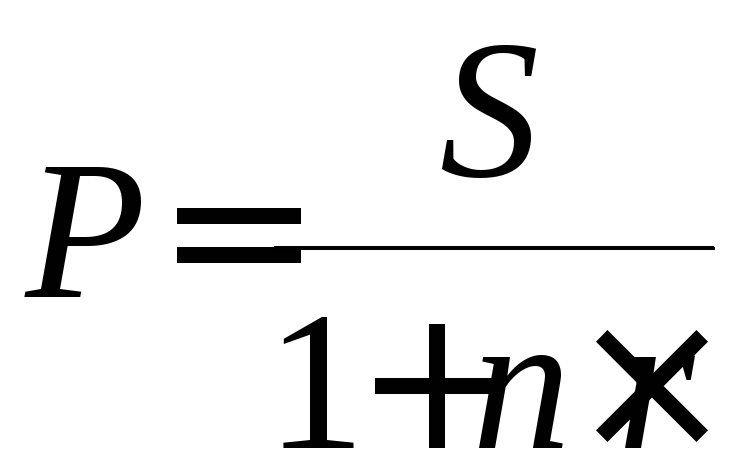 , (4)
, (4)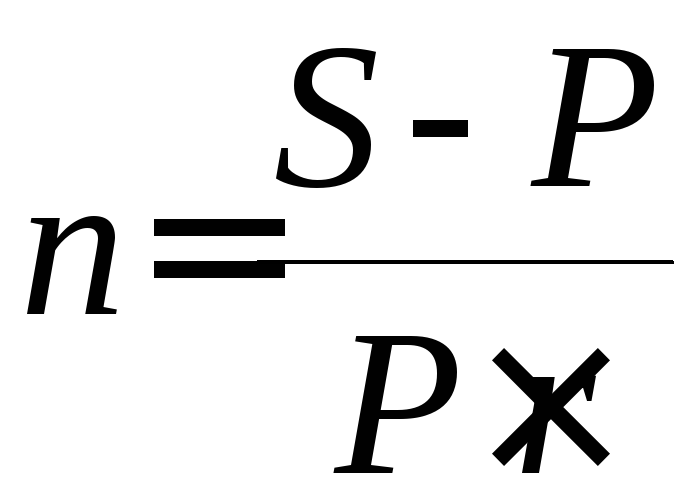 , (7)
, (7)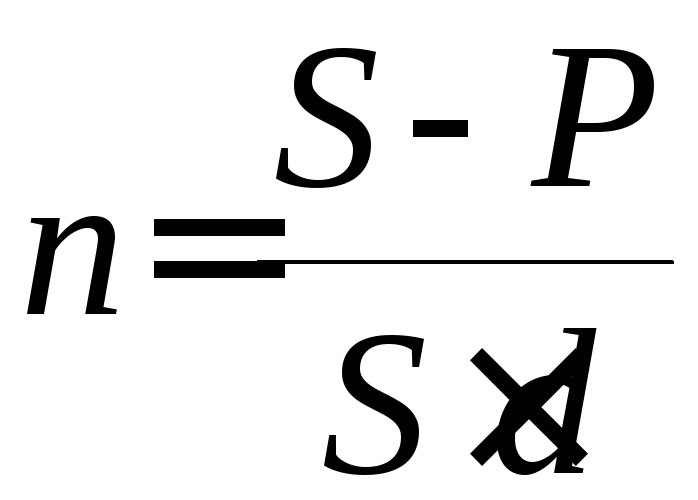 ,
(8)
,
(8)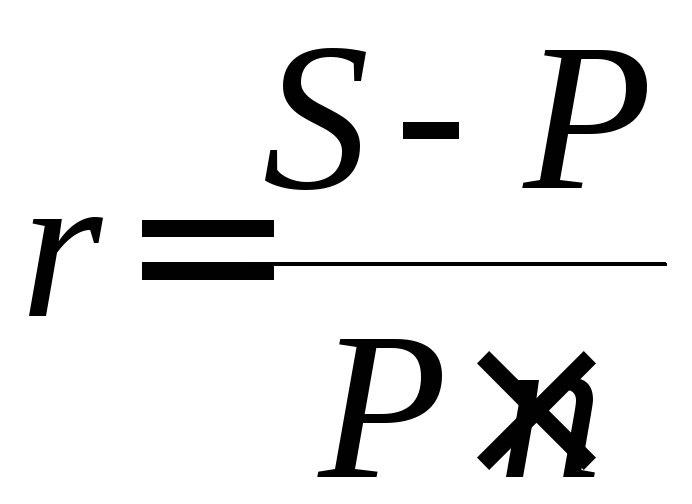 , (9)
, (9)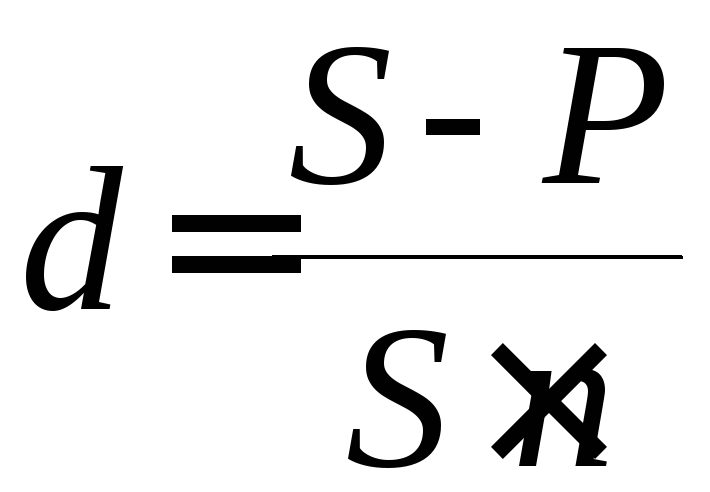 ,
(10)
,
(10)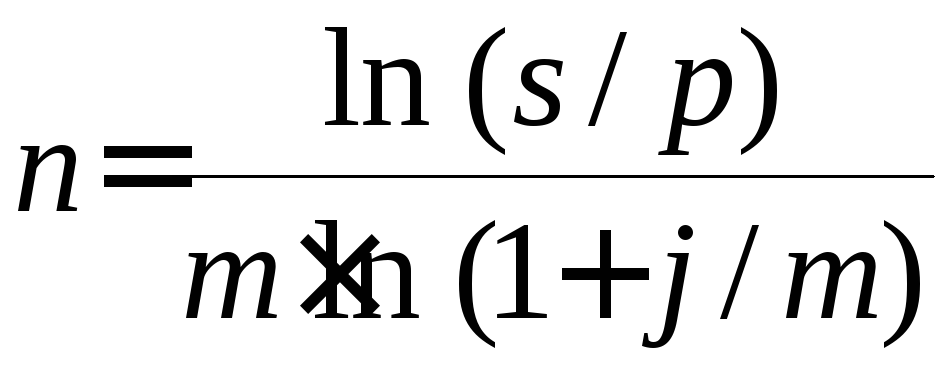 , (11)
, (11)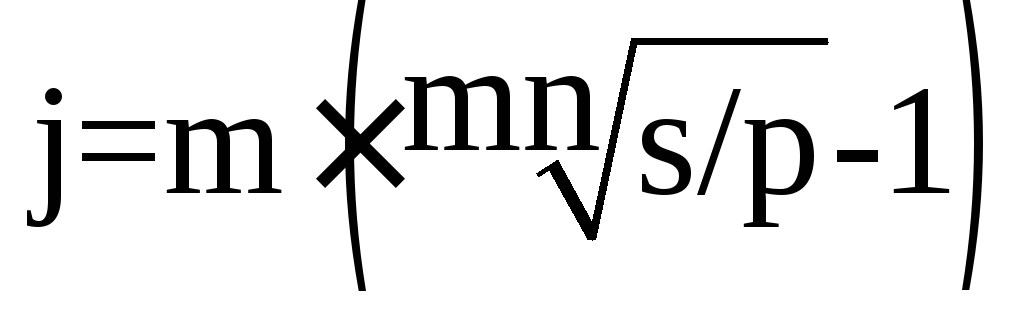 , (12)
, (12)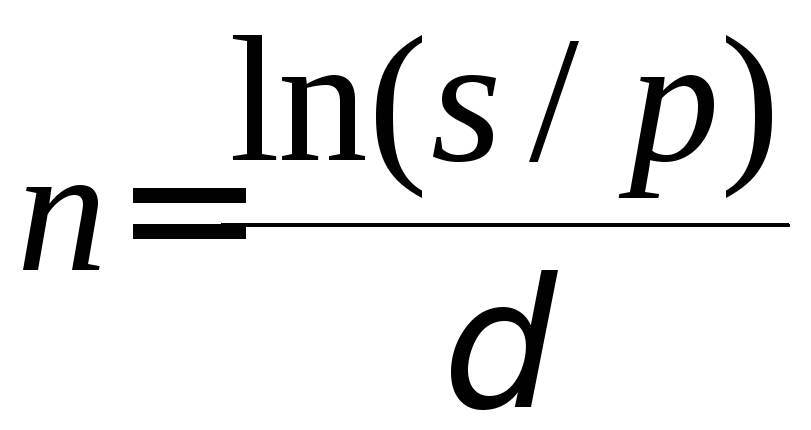 , (13)
, (13)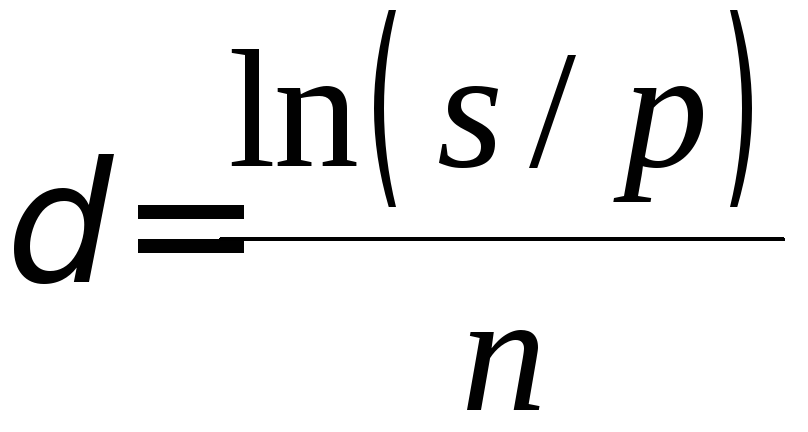 , (14)
, (14)