|
|
Примеры: | контрольные | курсовые | дипломные | отзывы |
|
Облигации и оценка стоимостиВиды облигаций в финансовой математикеКогда деньги занимаются путем выпуска облигаций, нет никаких теоретических причин устанавливать единственную дату выкупа облигаций. Поэтому компании, выпускающие облигации, могут решить выкупать облигации в рассрочку. Например, облигация с лицевой 136  стоимостью 100 млн рб за которую выплачиваются проценты с нормой j2 = 6% , может выкупаться следующим образом $ 20 млн рб через 10 лет, 30 млн рб через 15 лет и 50 млн рб через 20 лет. Естественно, процент по облигации выплачивается только за неоплаченную лицевую стоимость. Таким образом, за только что упомянутую облигацию выплачивалось бы 3 млн рб через каждые 6 месяцев в течение первых 10 лет, 2,4 млн рб в течение следующих 5 лет и 1,5 млн рб в течение последних 5 лет. Такие облигации называютсясерийными облигациями. Недолгое размышление позволяет уяснить, что приобретение серийной облигации эквивалентно покупке нескольких отдельных облигаций одновременно, и поэтому методы, развитые в предшествующих параграфах годятся для исследования различных задач, касающихся серийных облигаций. ПРИМЕР 1 Найти покупную цену серийной облигации, описанной выше, обеспечивающей 4% ,m = 2 . РЕШЕНИЕ Данная серийная облигация эквивалентна следующим трем с нормой 6% ,m = 2 с номиналами : 20 млн рб на 10 лет, 30 млн рб на 15 лет и 50 млн рб , выкупаемую через 20 лет. Соответствующие покупные цены равны P1 = 20 + (0,6 - 0,4)а20 2% = 23,27029 млн рб, P2 = 30 + (0,9 - 0,6)а30 2% = 36,71894 млн рб, P3 = 50 + (1,5 - 1,0)а40 2% = 63,67774 млн рб. Покупная цена серийной облигации поэтому равна P = P1 + P2 + P3 = 123,667 млн рб . Все облигации, рассматриваемые до сих пор, выкупались одним или более взносами, каждый из которых был кратным 1 млн рб. Однако нет никаких причин для того, чтобы лицевая стоимость облигации не могла выкупаться таким образом, чтобы выкуп плюс процентные платежи облигации образовывали аннуитет. Таким образом, контракты, которые предназначаются для погашения долга, основной суммы и процентов равными периодическими платежами, часто называются аннуитетными облигациями. Оформляемые различным образом аннуитетные облигации 137  являются контрактами, представляющими аннуитет, подписанный в форме облигации. ПРИМЕР 2 Основная сумма и проценты 100 миллионной облигации аннуитета будут выкупаться при нормеj1 = 5% десятью одинаковыми взносами. Сколько предложит потенциальный покупатель за эту облигацию, если он желает реализовать эффективную инвестиционную норму процента a) 4% , b) 5% , c) 6% ? ПРИМЕР Мы сначала определим, какими будут взносы платежей. Так как они будут образовывать обыкновенный аннуитет, мы имеем
Цена, которая предлагается за эту облигацию, является текущей стоимостью этих платежей, вычисленной для желаемой инвестиционной нормы. Следовательно, (a)P = 12,9505а10 4% = 105,0402 млн рб . (b)P = 12,9505а10 5% = 100,0000 млн рб . (c)P = 12,9505а10 6% = 95,3168 млн рб . Довольно очевидно, что все задачи, касающиеся облигаций аннуитетов, являются просто задачами аннуитетов, сформулированными в терминологии облигаций, и значит методы, развитые в главах по аннуитетам годятся для их решения. 138 Облигации в финансовой математикеОблигациейназывается ценная бумага, удостоверяющая внесение ее владельцем денежных средств и подтверждающая обязательство возместить ему номинальную стоимость ценной бумаги в предусмотренный в ней срок с уплатой фиксированного процента, если иное не предусмотрено условиями выкупа. Облигации относятся к категории ценных бумаг с фиксированным доходом, поскольку обязательства по обслуживанию долга носят фиксированный характер, т.е. инвестиционное учреждение обязуется периодически выплачивать фиксированный процент и фиксированную выкупную сумму по истечении установленного срока. Инвестирование в облигации надежно защищено от риска, благодаря тому факту, что облигации представляют собой долг. Если компания, выпустившая облигации, потерпит крах, то выплаты держателям облигаций будут производиться в первую очередь. Облигации с нулевым купоном (в частности, российские ГКО) - это облигации, по которым проценты не выплачиваются, но при выпуске им назначается цена на условиях дисконтирования по сравнению с номинальной стоимостью. Облигации характеризуются следующими параметрами: NOM - номинальной стоимостью; T - сроком до погашения; g - купонной процентной ставкой; m - числом выплат процентов в году; Pt - текущей рыночной ценой; Vt - действительной стоимостью; Yt - текущей доходностью; jtef - доходностью к погашению. Под курсом облигации понимается величина Стоимость облигации Одной из основных характеристик облигации является ее действительная (приведенная) стоимость, ориентируясь на которую покупатели и продавцы устанавливают свои цены на покупку и продажу облигации на рынке. Ожидаемый денежный поток платежей по облигациям состоит из выплат по процентам плюс выплата номинальной стоимости облигации при погашении. Действительная стоимость облигации определяется как современная величина этого потока платежей. Для облигации с выплатой процентов m раз в году и целой
величиной
где jt - банковская процентная ставка в момент времени t. Движение банковской процентной ставки и курсов облигаций происходит в противоположных направлениях. По сути дела, колебания банковской процентной ставки является единственной наиболее важной силой на рынке облигаций. Как видно из формулы, при росте банковской процентной ставки действительная стоимость облигации падает, а при убывании - возрастает. При большой процентной ставке потоки денежных средств в отдаленном будущем являются менее важными, поскольку инвестор получает большую часть денег в ближайшем будущем. Действительная стоимость облигации с выплатой купонных процентов два раза в год может рассчитываться по следующей более точной формуле:
Оценивание облигаций между датами начисления процентов в финансовой математикеФормулы для покупной цены (1) и(2) были получены для облигаций, покупаемых в день начисления процентов, когда продавец удерживает процентные платежи этого дня, а покупатель получает контракт, содержащий все будущие платежи за облигацию. Очевидно, облигации могут продаваться и покупаются в произвольные дни. Следовательно, нам необходим способ определения стоимости облигации между датами начисления процентов по облигации.
покупную цену облигации на предшествующую дату начисления процентов, обеспечивающую норму процента i ; пустьf будет дробной частью периода начисления процентов, которая истекла с момента предшествующей даты начисления; пусть такжеP будет стоимостью облигации на день продажи. ТогдаP0 иP являются стоимостями одного и того же контракта на различные даты и поэтому являются эквивалентными. Поэтому уравнение эквивалентности нам дает формулу
для точной стоимости облигации на дату продажи. 120  Ранее мы говорили, что когда рассматривается дробная часть периода начисления, для аппроксимации точного результата может применяться приближенная формула, основанная на использовании простого процента вместо сложного. Тогда
ПРИМЕР 1 Найти покупную цену на 16 июня 1990 г. для облигации с лицевой стоимостью 10 млн рб, выкупаемую по номинальной стоимости 1 октября 2015 г., и предусматривающую проценты с нормой 6% ,m = 2. РЕШЕНИЕ Предшествующая дата начисления процентов по облигации 1 апреля 1990 г. Число периодов начисления от этой даты до даты выкупа равно 51. Поэтому стоимость облигации на 1 апреля 1990 г. равна P0 = 10 + (0,35 - 0,30)a 5 1 3 % = 10 + 1,2976 = 11,2976 млн рб Считая по 30 дней в каждом месяце, определяем срок от 1 апреля по 16 июня равным 75 дней, так что f = 75/180 = 5/12 . Формула (4) тогда дает P = 11,2976 (1 + 0,03 (5/12)) = 11,2976 ? 1,0125 = 11,4388 млн рб Если бы мы применяли формулу (3) для вычисления точной стоимости, мы бы получили P = 11,2976 (1,03)5/12 = 11,2976 ? 1,01239 = 11,4376 млн рб Разница этих двух результатов равна 1200 рб ( 0,0105 % ).
покупной ценой облигации на предстоящую дату начисления процентов. В день предстоящего начисления процента будет произведена выплата 121 Приобретение облигаций на рынке в финансовой математикеОчень редко облигация может быть куплена так, чтобы обеспечить заданную норму процента. В большинстве случаев облигации покупаются на бирже облигаций, где они продаются через аукцион с более высоким предложением цены. Это делается через агентов, действующих в интересах продавца и покупателя. Потенциальный продавец инструктирует своего агента относительно минимально допустимой цены продажи, в то время как потенциальный покупатель сообщает своему агенту максимальную цену, которую он может заплатить. Агенты работают за комиссионные и естественно пытаются получить для своих клиентов наилучшую цену из возможных. Теперь необходимо напомнить, что когда облигация продана в день начисления процентов за облигацию, процентные платежи облигации,
облигации, даже когда облигация покупается между датами начисления процентов за облигацию. Таким образом, продавец имеет право на ту
продажи также изменяется в зависимости от близости предстоящей даты
126  На практике накопленный процент облигации вычисляется по простой формуле R' = f R , гдеf является дробной частью периода начисления, который уже истек. Например, если за облигацию выплачивается 300 тыс рб процентов каждые 6 месяцев, тогда через 45 дней после даты начисления процентов накопленный процент облигации был бы равен 45/180 ? 300 = 75 тыс рб. Наконец, так как облигации выпускаются различными достоинствами, обычно дается рыночная котировка на основе облигации на 1 млн рб , округленная к ближайшей одной восьмой. Таким образом, если рыночной котировкой является 105 1/4 , то рыночная цена пятимиллионной облигации была бы 5 ? (105 1/4) = 5,2625 млн рб, а покупная цена была бы 5,2625 млн рб плюс накопленный процент облигации, если он имелся. Пример 1
За Решение Рыночная цена былаQ = 5 ? 1,085 = 5,425 млн рб. Так как она была продана 1 апреля,f = 60/180 = 1/3. Тогда R' = fR = (1/3) ? 0,15 = 0,05 млн рб и окончательно P = Q + R' = 5,425 + 0,05 = 5,4750 млн рб. Пример 2
За Решение Покупная цена 15 июля 1988 г., обеспечивающая норму процентаj2 = 4% , равна P0 = 10 + (0,3 - 0,2)а23 2% = 10 + 1,8292 = 11,8292 млн рб 15 сентября, двумя месяцами позже, покупная цена будет 127 P = P0(1 +if) = 11,8292 (1 + 0,02 (1/3)) = 11,9081 млн рб Для определения Q мы используем(5). Накопленный процент облигации равенR' = f R = (1/3) ? 0,3 = 0,1 млн рб. Тогда изP = Q + R' имеем Q = P - R' = 11,9081 - 0,1 = 11,8081 млн рб. Сводя этот результат к одно миллионной облигации, мы получим рыночное предложение в виде 118,081, округляя которое с точностью до одной восьмой, получим 118 1/8. Другой способ вычисления Q состоит в интерполяции между значениямиP0 иP1 , где эти символы имеют то же самое значение, как и в предыдущем параграфе. Следует четко представлять, что обе формулы (4) и(5) дают одно и то же значение покупной ценыP . Выбор той или иной формулы зависит от известных данных. Таким образом, потенциальный покупатель, который решает, что он купит облигацию, если только она обеспечит ему, скажем, 4% или более, использовал бы формулу(4) для определения максимальной цены, которую он мог бы заплатить. Формула(5) или ее эквивалентQ = P - R' давали бы тогда соответствующую рыночную цену. Потенциальный продавец, однако, обычно определяет минимальную ценуQ , которую он бы допустил за будущие поступления от облигации. Эта цена не включает ту часть предстоящих процентных платежей облигацииR' , которые уже накоплены, и поэтому полную покупную цену следует определять по формуле(5).
процентов облигации. Оба эти термина используются одинаково часто и читателю следует знать, что они означают одно и то же. ВеличинаP , которую мы называли покупной ценой, почти всегда упоминается как прямая цена облигации. Методы, рассмотренные в последних параграфах, оставляют без ответа три важных вопроса : a) Если используется закон сложных процентов, каким будет накопленный процент облигации ?b) Какова точная формула дляQ ?c) Как построить инвестиционное расписание для облигации, покупаемой между датами начисления процентов ? Ответ на эти вопросы дается в следующем параграфе. 128  Расписания облигаций в финансовой математике | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Когда облигация покупается за сумму P , большую ее выкупной цены | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
C , разность |
P - C |
называется превышением, то есть превышением | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
покупной цены над ценой выкупа. До тех пор |
пока процентные платежи | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
облигации |
используются для амортизации |
превышения, происходит | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
потеря капитала на дату выкупа. В качестве иллюстрации предположим, что инвестор покупает облигацию с лицевой стоимостью 10 млн рб, за которую выплачиваются проценты с нормой 5% , m = 2 , и она выкупается в конце трехлетнего периода за 10,5 млн рб, принося доход 4% ,m = 2. По любой из формул(1) или(2) покупная цена определяется величиной 10,7241 млн рб. В конце каждых шести месяцев инвестор будет получать 0,25 млн рб процентных платежей облигации. Однако,
122
он в действительности не получает 0,25 млн рб каждые шесть
месяцев, так как в конце трехлетнего периода он получит только 10,5 млн рб
первоначальной суммы 10,7241 млн рб, инвестированной в облигацию. Это превышение
0,2241 млн рб должно быть сэкономлено из процентных платежей облигации для того,
чтобы возместить полностью всю основную сумму, инвестированную в облигацию.
Поэтому важно, чтобы был принят
|
Хотя существует несколько |
способов, используемых бухгалтерами |
|
для амортизации превышения, |
наиболее прямой способ основан на том |
факте, что облигация была куплена для получения инвестиционного дохода с данной нормой процента на деньги, инвестированные в облигацию. В приведенной выше иллюстрации покупная цена была определена так, чтобы облигация давала доход 2% каждые шесть месяцев на деньги, инвестированные в нее. Таким образом, в конце первой половины года процент инвестора должен был быть равным
10,7241 ? 0,02 = 0,2145 млн рб.
Так как он в действительности получил 0,25 млн рб, разность 0,0355 млн рб рассматривается как возмещенная часть первоначальной основной суммы. Следовательно, теперь облигация оценивается суммой
10&7241 - 0&0355 = 10&6886 млн рб. Эта книжная цена является той же самой, что и покупная цена облигации за два с половиной года до погашения в расчете на доход по норме 4% ,m = 2 , и может быть вычислена независимо по каждой из двух формул расчета покупной цены.
Повторяя вышеописанную процедуру, мы найдем, что процент
инвестора в конце второго
10,6886 ? 0,02 = 0,2138 млн рб .
Таким образом, 0,25 - 0,2138 = 0,0362 млн рб из второго процентного платежа облигации является возмещенной частью основной суммы и новой книжной ценой является 10,6886 - 0,0362 = 10&6524 млн рб. Такая вычислительная процедура повторяется до погашения облигации. Конечная книжная цена равна 10,5 млн рб, то есть является ценой выкупа. Эта информация может быть представлена в виде таблицы, которая называется расписанием облигации. Приведем пример расписания облигации для только что рассмотренного случая.
Расписание облигации, купленной с превышением
123
|
Конец |
Платежи |
Процент |
Амортизация |
Книжная |
|
периода |
процентов |
инвестора |
превышения |
цена |
|
0 |
|
|
|
10,7241 |
|
1 |
0,25 |
0,2145 |
0,0355 |
10,6886 |
|
2 |
0,25 |
0,2138 |
0,0362 |
10,6524 |
|
3 |
0,25 |
0,2130 |
0,0370 |
10,6154 |
|
4 |
0,25 |
0,2123 |
0,0384 |
10,5777 |
|
5 |
0,25 |
0,2116 |
0,0384 |
10,5393 |
|
6 |
0,25 |
0,2108 |
0,0392 |
10,5000 |
|
Всего |
1,50 |
1,2760 |
0,2240 |
|
Когда облигация покупается за цену, меньшую, чем ее цена выкупа, разность C - P называетсядефицитом. Например, предположим, что облигация в описанной нами иллюстрации была куплена за три года до погашения с целью получения дохода с нормой 6% ,m = 2. В этом случае формулы(1) или(2) дают требуемую покупную цену 10,1479 млн рб. Так как облигация будет выкупаться за 10,50 млн рб, дефицит равен
10,50 - 10,1479 = 0,3521 млн рб.
Когда облигация покупается с дефицитом, инвестор выигрывает больше, чем непосредственные процентные платежи облигации, так как облигация выкупается за большую цену, чем первоначальная покупная цена. Хорошая расчетная практика требует, чтобы это увеличение стоимости облигации накапливалось постепенно. Таким образом, необходим какой либо систематический план накопления дефицита. Имеется несколько способов сделать это. Наиболее прямой из них использует тот факт, что облигация должна обеспечивать заданную норму процентов на сумму денег, инвестированную в облигацию. Для
|
иллюстрации этого метода мы |
сконструируем расписание облигации | |||
|
для облигации, |
использованной |
в предыдущей |
иллюстрации, |
но |
|
купленной по |
цене, обеспечивающей норму 6% , |
m = 2. В этом случае | ||
|
покупная цена была бы 10,1479 , то есть облигация продавалась бы |
с | |||
дефицитом 0,3521. Поэтому процент инвестора в конце 6 месяцев равен
10,1479 ? 0,03 = 0,3044 млн рб.
Так как процентные платежи облигации равны 0,25 млн рб, стоимость облигации увеличивается на
0,3044 - 0,25 = 0,0544 млн рб.
124
Книжная цена облигации становится равной 10,2023 млн рб. Следует заметить, что процент инвестора в данном случае состоит из двух частей: a) процентные платежи облигации и b) увеличение в стоимости облигации. Эта последняя часть будет получена при выкупе облигации.
В конце второго периода начисления процент инвестора будет равен
102023 ? 0,03 = 0,3061 млн рб;
увеличение стоимости облигации будет равно 0,3061 - 0,25 = 0,0561 млн рб; новая книжная цена станет равной
10,2023 + 0,0561 = 10,2584 млн рб.
Эта процедура продолжается до погашения облигации, во время которого окончательная книжная цена станет равной 10,50 млн рб, то есть совпадет с покупной ценой. Следующая таблица дает полное расписание только что рассмотренной облигации.
Расписание облигации, купленной с дефицитом
|
Конец |
Платежи |
Проценты |
Накопление |
Книжная |
|
периода |
процентов |
инвестора |
дефицита |
цена |
|
0 |
|
|
|
10,1479 |
|
1 |
0,25 |
0,3044 |
0,0544 |
10,2023 |
|
2 |
0,25 |
0,3061 |
0,0561 |
10,2584 |
|
3 |
0,25 |
0,3078 |
0,0578 |
10,3162 |
|
4 |
0,25 |
0,3095 |
0,0595 |
10,3757 |
|
5 |
0,25 |
0,3113 |
0,0613 |
10,4370 |
|
6 |
0,25 |
0,3131 |
0,0631 |
10,5000 |
|
Всего |
1,50 |
1,8522 |
0,3522 |
|
Несколько замечаний относительно современной терминологии. Разность
|
P - F |
определена как премия, а разность |
P - C - как |
превышение. | |||||
|
Когда |
облигация |
выкупается |
по номинальной стоимости, премия и | |||||
|
превышение |
одинаковы; |
в других случаях это не выполняется. Так как | ||||||
|
большинство |
облигаций |
выкупается по |
номинальной |
стоимости, | ||||
|
процесс выписывания превышения покупной |
цены над ценой выкупа | |||||||
|
часто называется амортизацией |
премии. Подобным образом, дисконт | |||||||
|
F - P |
и дефицит |
C |
- P |
являются одинаковыми для облигаций, | ||||
|
выкупаемых по номинальной стоимости, |
так |
что слова |
«накопление | |||||
|
дисконта» часто используются |
для обозначения накопления дефицита. | |||||||
125
Таблицы облигаций в финансовой математике
135
Чтобы дать представление о покупной цене облигации для большого разнообразия норм доходности, должны быть подготовлены подробные таблицы. Пример такой таблицы приводится ниже.
Когда таблицы имеются под рукой, многие проблемы облигаций могут быть решены при помощи простого взгляда на них. Более того, так как нормы доходности табулированы для значений, которые различаются только на 0,05 % , интерполяция промежуточных значений дает высокую точность.
Так как разнообразное использование таблиц довольно очевидно, в иллюстративных примерах нет надобности. Однако следует подчеркнуть, что не все задачи об облигациях можно решить с использованием таблиц и, следовательно, крайне желательно знание всех методов, рассмотренных в предшествующей части настоящей главы.
Покупная цена облигации с номинальной стоимостью 10 млн рб,
|
за которую выплачивается процент с нормой |
j2 = 4% . |
| ||
|
| ||||
|
Норма |
Время до выкупа, годы | |||
|
доходности |
|
|
|
|
|
(m = 2) |
8 |
8,5 |
9 |
9,5 |
|
| ||||
|
3,25% |
10,5246 |
10,5531 |
10,5812 |
10,6088 |
|
3,30% |
10,4887 |
10,5152 |
10,5412 |
10,5669 |
|
3,35% |
10,4529 |
10,4774 |
10,5015 |
10,5252 |
|
3,40% |
10,4172 |
10,4397 |
10,4619 |
10,4836 |
|
... |
... |
... |
... |
... |
|
3,85% |
10,1024 |
10,1079 |
10,1132 |
10,1184 |
|
3,90% |
10,0682 |
10,0718 |
10,0753 |
10,0788 |
|
3,95% |
10,0340 |
10,0358 |
10,0376 |
10,0393 |
|
4,00% |
10,0000 |
10,0000 |
10,0000 |
10,0000 |
Учет векселей в финансовой математике
Банковский учет применяется при операции по учету векселей банком или другим финансовым учреждением. Вексель - это подписанное обязательство заемщика уплатить в указанный срок определенную сумму предъявителю векселя или лицу, указанному в векселе. Суть операции учета векселя заключается в следующем: банк до наступления срока платежа по векселю приобретает его у владельца по цене, которая меньше суммы, указанной на векселе, то есть, покупает (учитывает) его с дисконтом (со скидкой), получая при наступлении срока платежа по векселю деньги в сумме, указанной на векселе, банк реализует дисконт. При этом применяется банковский учет: проценты в виде дисконта начисляются на сумму, подлежащую уплате в конце срока
Для подсчета получаемой при учете векселя суммы в случае простой учетной ставки d используется формула (42). Примем момент выдачи векселя за нулевой; Т - общий срок обязательства; N - указанная на векселе сумма (номинал векселя). Пусть операция учета векселя производится в момент времени t, так что оставшийся до погашения векселя срок равен Т-t. Тогда сумма St, получаемая владельцем векселя при его учете (стоимость векселя в момент времени T) определяется по формуле:
![]() (47)
(47)
Дисконт Dt при этом равен:
Dt=N·d·(T-t).
Если срок до погашения векселя измеряется в днях, то принимают
Т - t =?/К , где ? -количество дней до погашения векселя, К - временная база (чаще всего используются обычные проценты с точным числом дней ссуды). Формула расчета стоимости векселя принимает вид:
![]()
Пусть теперь вексель после его покупки и до наступления срока погашения продан. Эффективность (доходность) этой операции можно измерить, например, в виде ставки простых или сложных процентов. Пусть номинал векселя равен N , и он куплен (учтен) по простой учетной ставке d1 за ?1 дней до наступления срока. Цена в момент покупки равна
![]()
Пусть далее тот же вексель за ?2 дней до погашения продан с дисконтированием по ставке d2 по цене:
![]()
Таким образом, в начале операции инвестирована сумма S1, в конце операции получена сумма S2, длительность операции ?1-?2 дней. Определим годовую ставку iэ простых процентов, обеспечивающую эквивалентный финансовый результат, из уравнения
![]()
Откуда выводим:
![]() (48)
(48)
Ставка iэ определяет эффективность (доходность) финансовой операции покупки и продажи векселя. Если S2< S1,то операция убыточна. Показатель доходности операции покупки векселя с последующим его погашением определяется по этой же формуле при ?2=0, S2=N.
При учете векселя может использоваться сложная учетная ставка. По формуле (44) находим стоимость векселя в момент времени t:
![]() (49)
(49)
В качестве меры доходности операции переучета векселя можно также использовать сложную годовую ставку процентов. Для ее определения составим уравнение:
![]()
где Т =(?1-?2) /К – срок операции, S1 – цена векселя в момент покупки, S2 – цена, по которой он был продан. Отсюда получаем явное выражение для показателя доходности iэ:
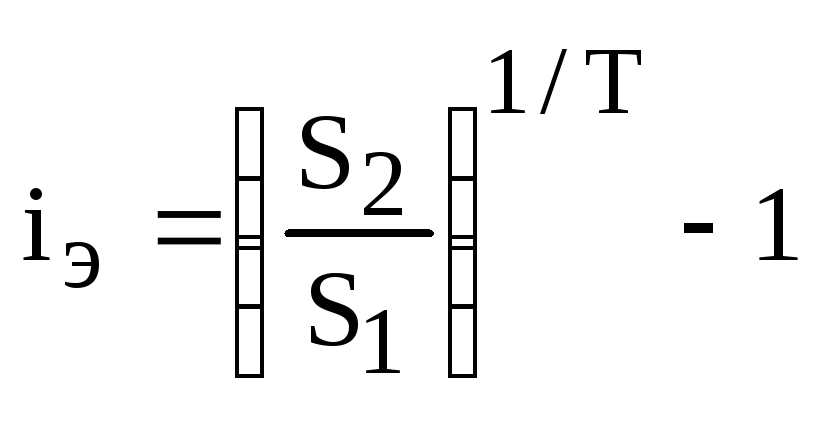
Доходность операции покупки векселя с последующим его погашением определяется тем же способом при ?2=0, S2=N.
Цена облигации между датами начисления процентов в финансовой математике
|
Ранее мы отмечали, что точная стоимость облигации |
между датами | |
|
начисления дается формулой P = P0 (1 + |
i)f , гдеP0 |
представляет |
|
стоимость облигации в предшествующую |
дату начисления, i - норма | |
|
доходности облигации и f является дробной частью периода начисления, | ||
которая истекла после последней даты начисления. Теперь мы получим точную формулу для определения накопленного процента облигации R' .
Если использовать точный метод, понятно, что покупателю и продавцу следует разделить предстоящую выплату процентов облигации соответственно закону сложных процентов. Пусть R' будет долей продавца, полагающейся в день продажи, аR" будет долей покупателя, полагающейся в предстоящую дату начисления процентов. Эти две
|
доли должны |
быть эквивалентными |
процентному платежу |
облигации |
|
R , делаемому в конце периода, как показано на диаграмме |
| ||
|
|
R' |
R" |
|
|
f |
1 – f |
R |
|
|
|
|
| |
|
Равенство стоимостей на конец периода дает |
| ||
|
|
R' (1 +i)1 – f |
+ R" = R |
(a) |
Так как обе доли R' иR"
неизвестны, нам нужно иметь еще одно соотношение между ними, для того,
чтобы однозначно определить их значения. Второе соотношение может быть получено
путем следующих рассуждений. Так как определениеR'
иR" должно быть справедливым как для покупателя
так и для продавца, перестановка временных интерваловf
и
R" R'
|
1 – f |
f |
R
129

Равенство стоимостей в конце периода теперь дает
R' + R"(1 + i) = R
Если равенство (a) умножить на (1 +i)f , мы получим
R'(1 +i) +R"(1 +i)f =R (1 +i)f .
Теперь вычитая равенство (b) из (c), найдем, что
R'i = R(1 + i) f - R
Отсюда R' определяется в следующем виде
|
R R |
1 i f 1 |
Rs |
|
|
i . | ||
|
i |
| ||||||
|
f |
| ||||||
|
|
|
|
|
| |||
Подобным образом получим R Rs1 f i .
(b)
(c)
(6)
Пример За облигацию выплачивается 300 тыс рб процентных денег каждые 6 месяцев. Каков накопленный процент облигации двумя месяцами позже даты начисления, если норма доходности равнаa) 4% ,m = 2;b) 8% ,m = 2 ?
Решение a) Двумя месяцами позже даты начисленияf = 1/3. Значит
R Rsf i 30s1/3 2% = 300 ? 0,33113548 = 99,34 тыс рб .
b) Для нормы доходности 8% ,m = 2 мы имеем
R' = 300 ? 0,3289851 = 98,7 тыс рб .
Практический способ вычисления дает
R' = fR = (1/3) ? 300 = 100 тыс рб .
Можно показать, что значение R' , полученное из точного равенства(6) всегда несколько меньше, чем то, которое дается приближенной (практической) формулойR' = f R . Однако разность является обычно
130

малой и так как покупатели на одну дату становятся продавцами на другую дату, большой несправедливости не ощущается при использовании простой формулы.
Так как точная формула (6) дляR' найдена, теперь можно получить точную формулу дляQ . Начнем с равенстваP = Q + R' илиQ =P - R'. Используя равенства(3) и(6) для исключенияP иR' , получим
Q = P0 (1 +i)f –Rsf i
Теперь при помощи (1) исключаемP0 . Это дает
Q = (C(1 +i)
Или после преобразования
Q = C(1 +i)
Используя одно из тождеств для функций составных платежей:
an k i= (1 + i) k an isk i ,
последнее выражение можно представить в упрощенной форме:
|
Q = C(1 +i) |
|
|
i . |
(7) |
|
n f |
|
Путем использования точно такой же процедуры, какую мы использовали в параграфе 8.4, формулу (7) можно преобразовать к следующему виду
|
Q = C + (R - Ci) a |
|
|
i . |
(8) |
|
n f |
|
Таким образом, формулы для Q являются точно такими же, как(1) и(2) дляP , только время, оставшееся до погашения, содержит дробные части периода. С точки зрения смысла, который будет приписан функцииa n i в параграфе 10.2 для дробных значенийn , формула(7) показывает,
что Q равна настоящей стоимости цены выкупа плюс настоящая стоимость будущих процентов облигации и не включает часть текущего
131

процентного платежа облигации, которая уже накоплена. Поэтому покупная цена должна быть P = Q + R' .
Проиллюстрируем эти аналитические формулы численным примером. Предположим, что за облигацию 10 млн рб выплачивается 0,3 млн рб процентов каждые 6 месяцев и она продается за 10 лет и 3 месяца до даты выкупа по номинальной стоимости, чтобы приносить проценты по норме j = 4% . Находим, что
|
|
P0 = 10 + (0,3 - 0,2)a |
|
|
2% = 11,70112 млн рб , | |
|
|
21 |
| |||
|
|
P = P0(1 +i)f = 11,70112 (1,02)0,5 = 11,81755 млн рб . | ||||
|
Таким |
образом, покупная цена |
облигации должна быть 11,81755 млн | |||
|
рб. Однако эта сумма должна |
рассматриваться как состоящая из двух | ||||
|
частей, |
а именно : накопленный процент облигации | ||||
R' = 0,3s0,5 2% = 0,14926 млн рб
и рыночная цена Q = P - R' =
11,66829 млн рб. На следующую дату начисления процентный платеж облигации
подобным образом рассматривается состоящим из нескольких
частей.
R'(1 +
Q(1 +
Остаток процентного платежа облигации, а именно :
0,3 – 0,15075 – 0,11611 = 0,03314 млн рб
является амортизацией премии и уменьшает книжную стоимость облигации до 11,66829 – 0,03314 = 11,63515 млн рб. Можно проверить, что значение, полученное для Q , является точно таким же, которое получается по формуле(7) или(8), и что окончательная книжная стоимость 11,63515 млн рб является величинойP .
132
Список литературы и источников на тему "Облигации и оценка стоимости"
- Cписок курсовых работ по оценке товарных знаков (2016 г.)
- Курсовая работа по оценке товарного знака на примере товарного знака нефтяной терминал
- Курсовая работа по оценке товарного знака на примере товарного знака МИСТРАЛЬ
- Курсовая работа по оценке товарного знака на примере товарного знака МАКФА
Другие похожие работы
© 2002 - 2024 RefMag.ru
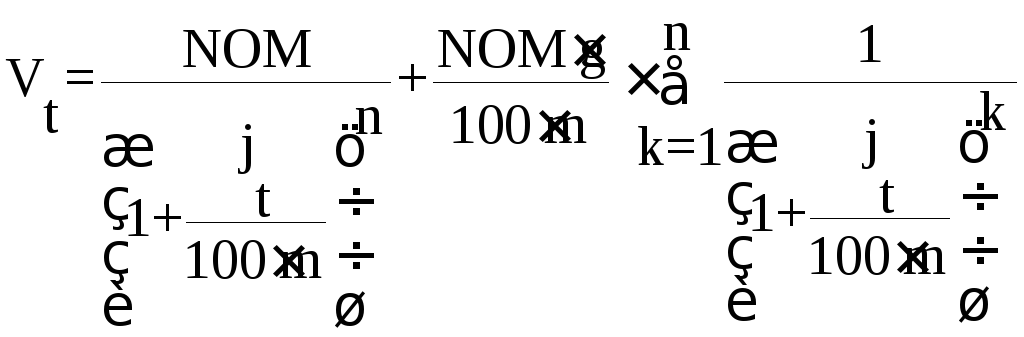 , (30)
, (30)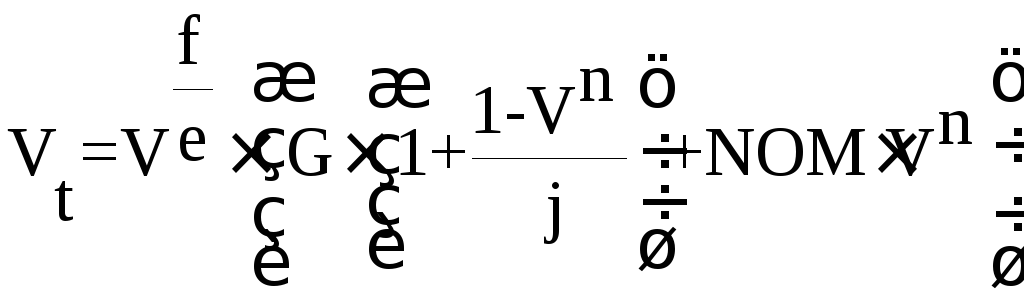 , (31)
, (31)