|
|
Примеры: | контрольные | курсовые | дипломные | отзывы |
|
Кредит в оценке стоимостиЛьготные займы и кредиты и финансовая математикаВряде случаев
долгосрочные займы и кредиты выдаются на льготных для заемщика условиях. Низкая
процентная ставка по сравнению с рыночной в сочетании с большим сроком и
наличием льготного периода дают должнику существенную выгоду, которую можно
рассматривать как субсидию. Такая субсидия оказывается как на международном
уровне в рамках финансовой помощи развивающимся странам, так и внутри страны для
поддержки отдельных отраслей или производств. Проблема определения размера этой
помощи сводится к оценке Абсолютный Абсолютный А относительный w =WD =1?GD , где W –
абсолютный G – современная величина платежей, рассчитанная по реальной ставке рынка кре- дитов. 57 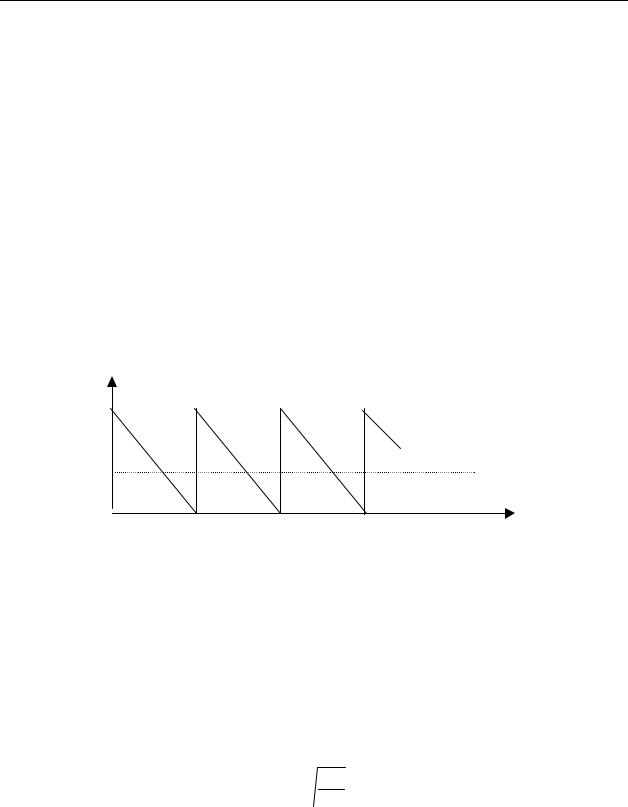 АНАЛИЗ ФИНАНСОВЫХ ПОТОКОВ Раздел III. Потоки платежей в производственной деятельности Виды погашения долга (кредита)В этом параграфе дается применение теории рент к планированию погашения займа (долга). Разработка плана погашения займа заключается в составлении графика периодических платежей должника. Расходы должника называются расходами по обслуживанию долга или амортизацией займа. Эти расходы включают как текущие процентные платежи, так и средства, предназначенные для погашения основного долга.Существуют различные способы погашения долга. Участники кредитной сделки оговаривают их при заключении контракта. В соответствии с условиями контракта составляется план погашения задолженности. Важнейшим элементом плана является определение числа выплат в течение года, т.е. определение числа срочных уплат и их величины.
53 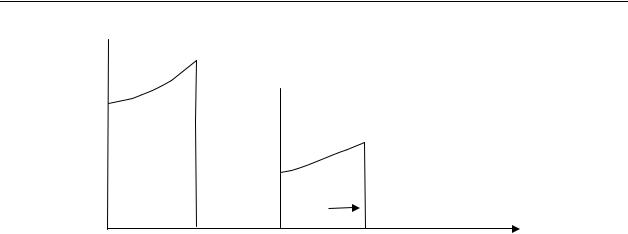 АНАЛИЗ ФИНАНСОВЫХ ПОТОКОВ R1 R2 К0К1 R3 К2
Т Рис. 2.1. Контур кредитной операции Для контура, показанного на рис.2.1, получим следующие расчетные формулы K1 = K0(1+i )t1 ?R1 , K2 = K1(1+i )t2 ?R2 , K2(1+i )t3 ?R3 = 0, где K0
- первоначальная сумма долга,R1
иR2
( K0qt1 ?R1 )qt2 ?R2 qt3 ?R3 = 0 , которое нетрудно привести к следующему виду K0qT ?( R1qt2 +t3 + R2qt3 + R3 )= 0 , где T=?tj, q=1/(1+i). В этом уравнении методологически ясно представлены два процесса: наращение первоначальной задолженности за весь период и наращение погасительных платежей за срок от момента платежа до конца срока операции. Таким образом, полученное уравнение отражает баланс сумм, наращенных на момент времени T. Умножим это уравнение на дисконтный множительvT K0 ?(R1vt1 + R2vt1 +t2 + R3vT ) = 0 , В этом виде уравнение выражает равенство суммы современных величин погасительных платежей сумме кредита, то есть баланс современных величин. Эти уравнения нетрудно обобщить на случай n погасительных платежей. Методы оценки показателей
доходности для разных видов 2.2. Доходность ссудных и учетных операций, предполагающих удержание комиссионных 54  АНАЛИЗ ФИНАНСОВЫХ ПОТОКОВ Ссудные операции. За открытие кредита, учет векселей и другие операции кредитор часто взимает комиссионные, которые повышают доходность операций, так как размер фактически выданной ссуды сокращается. Пусть ссуда в размере D выдана на
срокn, и при ее выдаче из нее удерживаются
комиссионные в размереG. Фактически выданная ссуда
равна Рассмотрим сначала сделки с начислением простых процентов по ставке i. Обозначим черезiэ,пр – фактическую доходность, выраженную через ставку простых процентов, и пустьg – относительная величина комиссионных в сумме кредита, то естьG=Dg. Тогда из балансового уравнения находим
Теперь рассмотрим долгосрочную операцию, когда ссуда с удержанием комиссионных выдается под сложные проценты. Тогда балансовое уравнение имеет вид Откуда
Учетные операции. Рассмотрим полную доходность банка при осуществлении операции учета с удержанием комиссионных. Пусть при учете применяется простая учетная ставка. После
удержания комиссионных и дисконта заемщик получает сумму Откуда полная доходность
Кредитные операции и финансовая математикаДоходы от Отметим, что при получении кредита должник может оплачивать комиссионные или другие разовые расходы (посреднику), которые увеличивают цену кредита, но не меняют доходность кредитора. Определение неоплаченной суммы долга в финансовой математике
79  Неоплаченная сумма долга на любую дату представляет собой невозмещенный баланс долга. Точно так же на любую дату настоящая стоимость платежей, которые еще не сделаны, представляет собой невозмещенный баланс долга. Таким образом, мы получаем следующее соотношение эквивалентности : неоплаченная сумма долга на любую заданную дату эквивалентна сумме платежей, которые должны быть сделаны. ПРИМЕР 1 Долг 100 млн рб будет амортизироваться платежами в конце каждого квартала в течение 12,5 лет. Если деньги стоят 3,5 % ,m = 4, найти неоплаченную часть долга в конце седьмого года. РЕШЕНИЕ Способ 1. Сначала определим необходимые амортизационные платежи. Платежи образуют обыкновенный аннуитет с текущей стоимостью 100 млн рб, поэтому
Так как неоплаченная часть долга в конце
Равенство стоимостей дает P = R а22 7/8% = 2,4779 ? 19,93310 = 49,3923 млн рб.
80  Заметим, что на временной диаграмме в конце седьмого года
помещено P, обозначающее остающиеся платежи. Теперь мы
составим уравнение стоимостей на конец P + R s50 7/8% = 100 ? (1,00875)28 . Разрешая его относительно P , мы получим P = 100(1,000875)28 - 2,4779s50 7/8% = 49,3923 млн рб . При определении неуплаченной части долга мы использовали
два подхода. В первом использовалась заключительная часть временной диаграммы и
платежи, еще не сделанные. Такой способ иногда называют методом перспективы, так как он использует будущие операции
по выплате долга. Во втором способе используется начальная часть временной
диаграммы и платежи, которые уже сделаны. Так как этот способ использует уже
выполненные операции по выплате долга, его иногда называютретроспективным методом. Когда все платежи одинаковые,
обычно проще использовать первый метод, так как неоплаченная часть долга в любой
момент времени совпадает с настоящей стоимостью аннуитета, состоящего из
платежей, которые еще предстоит сделать. Таким образом, сразу после
81  ( При вычислении по этой формуле, к тому же, достаточно пользоваться одной таблицей. ) Эта формула показывает также , что выплаченная сумма долга равна (R - Ai)s k i . ПРИМЕР 2 Долг 300 млн рб и проценты приj12 = 6% амортизируются платежами по 5 млн рб в конце каждого месяца до полного погашения долга. Найти неоплаченную часть долга в конце третьего года. РЕШЕНИЕ Так как число платежей и величина заключительного платежа неизвестны, проще использовать ретроспективный метод. ПустьP обозначает неоплаченную часть долга в конце третьего года. ТогдаP эквивалентно всем платежам, сделанным после трех лет, и может быть использовано для обозначения всех этих платежей на временной диаграмме
300 Записывая уравнение эквивалентности с использованием конца
P + 5s36 0,5% = 300 ? (1,005)36. Производя вычисления, получим P =
162,324 млн рб. Метод амортизации часто используется при ликвидации долга,
возникающего
Слова «стоимость собственности» относится к первоначальной продажной цене, которая может быть или не быть ее настоящей рыночной стоимостью.
82 
которые ежемесячно выплачиваются. Неоплаченная часть стоимости дома в конце 6 лет может быть найдена или методом перспективы или ретроспективным методом, но метод перспектив в этом случае будет проще. Представим выплаты за последние 9 лет на временной диаграмме
Приравнивание стоимостей дает P = R а180 1/2% = 0,5907 ? 83,29342446 = 49,2014 млн рб, которые являются неоплаченной частью стоимости дома, или долей продавца в конце 6 лет. Так как первоначальная цена дома была 100 млн рб, доля покупателя равна 100 - 49,2014 = 50,7986 млн рб.
аннуитет. Таким образом, мы имеем R = W/s
m = 0,5 ? 12,27257753 = 6,136289 млн рб, 83 Планирование погашения долгосрочной задолженности в финансовой математикеПри значительных размерах задолженности долг обычно погашается в рассрочку, частями. Разработка плана погашения займа заключается в составлении графика периодических платежей должника (срочных уплат), включающих как средства, предназначенные для погашения основного долга, так и текущие процентные платежи. Рассмотрим два основных способа погашения долга. 1). Погашения основного долга равными суммами. Пусть долг в сумме D погашается в течение n лет, и пусть проценты выплачиваются каждый раз в конце года по ставке i. В этом случае сумма, ежегодно идущая на погашения основного долга, составит d = D / n . Размер долга при этом последовательно сокращается: D, D-d, D-2d, ..., 0. Уменьшается и сумма выплачиваемых процентов, так как они начисляются на остаток долга. Пример. Долг в сумме 12000 руб. необходимо погасить последовательными равными суммами за 3 года платежами постнумерандо. За заем выплачиваются проценты по ставке 20% годовых. План погашения долга представлен ниже. Цифры внизу таблицы указывают порядок заполнения ее столбцов.
(1) (3) (4) (2) 2). Погашение долга равными срочными уплатами. Согласно этому методу расход должника по обслуживанию долга (срочные уплаты) постоянны на протяжении всего срока погашения. Из каждой срочной уплаты часть выделяется на уплату процентов, а остаток идет на погашение основного долга. Для разработки плана погашения нужно сначала определить размер срочной уплаты, а затем разбить каждую из срочных уплат на процентные платежи и сумму, идущую на погашение основного долга. Пусть срок погашения займа n лет, и проценты начисляются в конце каждого года по ставке i . Обозначим сумму каждой срочной уплаты через R . Периодическая выплата в конце каждого года суммы R представляет собой постоянную годовую ренту постнумерандо. Приравнивая сумму долга D к современной величине этой ренты, найдем величину срочной уплаты:
Пример. Долг в сумме 12000 необходимо погасить равными срочными уплатами за 3 года платежами постнумерандо. За заем выплачиваются проценты по ставке 20% годовых. План погашения долга представлен ниже.
(3) (2) (1) (4) При заполнении таблицы сначала вычисляется размер ежегодной срочной уплаты, затем на остаток долга начисляются проценты, далее вычисляется сумма, идущая на погашение основного долга (разность между срочной уплатой и процентами за кредит), после этого вычисляется новый остаток долга. Планирование погашения долгосрочной задолженности в финансовой математикеПланирование погашения долгосрочной задолженности в финансовой математикеВажное практическое приложение теории аннутентов – составление различных вариантов (планов) погашения задолженности. При составлении плана погашения возникает необходимость в определение размеров платежей заемщика – выплаты процентов и выплаты по погашению основного долга при различных условиях погашения (амортизации, такие платежи носят название срочных уплат). В практике финансовых отношений заемщика и кредитора возможны следующие варианты погашения задолженности: 1) Займы без обязательного погашения, по которым постоянно выплачиваются проценты. В данном случае необходимо определить размер платежа при заданной процентной ставке (случай вечного аннутента). Размер платежа определяется из формулы современной величины вечного аннутента R = A *ic (5.1) 2) Погашение долга в один срок Если заемщик должен вернуть всю сумму долга в конце срока, целесообразнее бывает создание погасительного (амортизационного) фонда, для чего вносятся в банк определенные суммы, на которые начисляются проценты. Для дальнейшей записи формул введем обозначения: D – Основная сумм долга; gc – ставка процентов по займу, g - льготная процентная ставка, по которой предоставлен кредит; J – сумма процентов по займу; R – разовый взнос в погасительный фонд (годовые расходы по погашению основного долга) ic – ставка процентов на взносы в погасительный фонд;
Общая сумма долга по формуле сложных процентов составит:
3) погашение основго долга равными суммами (проценты периодически выплачиваются). Тогда на погашение постоянно идут платежи размером Д/n, а процентные выплаты ежегодно сокращаются, так как уменьшается основная сумма долга. Для определения размера срочной уплаты и процентного платежа после любого (к-ого) года:
4) Погашение долга с использованием постоянных срочных уплат
Периодическая выплата постоянной суммы «
5) Во многих случаях предпочтительнее оказывается погашение долга с использованием переменных срочных уплат. Срочные уплаты могут изменяться в соответствии с некоторой закономерностью или задаваться графиком погашения. 6) На практике часто встречается случай, когда заранее задаются размеры всех срочных уплат, кроме последней, определяемой величиной остатка долга на начало последнего периода. 7) Возможно изменение условий погашения кредитов (конверсия займа). При этом могут изменяться срок погашения займа, процентная ставка, порядок годовых выплат и т.д. При любом методе конверсии первоначально определяется сумма выплаченного основного долга и величина непогашенной его части. Непогашенная часть долга рассматривается как новый долг, подлежащий уплате на новых условиях. 8) В финансовой практике может возникнуть ситуация, когда кредитору, предоставившему несколько займов одному заемщику, удобно объединить эти займы в один, то есть произвести их консолидацию. Первым шагом при консолидации займов является нахождение величин остатков каждого долга. Рассчитав остатки долгов и просуммировав их, получают объединенный долг, на который составляется новый план погашения. 9) Иногда долгосрочные кредиты выдаются на льготных условиях (политические, социальные или иные соображения). Как правило, в данном случае кредит предоставляется по ставке значительно ниже рыночной на данный момент. В результате предоставления подобной льготы заемщик фактически получает субсидию. Кредитор же теряет определенную сумму в результате этой сделки. Эта добровольно упущенная выгода кредитора называется грант – элементом. Он может быть подсчитан в виде абсолютной или относительной величины. Абсолютный гран-элемент определяется по формуле:
где абсолютный грант-элемент может быть определен как разность между номинальной суммой (D) кредита и современной величиной погасительных платежей и выплаченных процентов (G), то есть:
Относительный гран элемент равен: 10) Погашение ипотечной ссуды. При составлении плана погашения ипотечной ссуды решаются задачи, аналогичные погашению долгосрочных займов, - определение размеров срочных уплат и остатка задолженности на любой момент времени. Например, погашение равными ежемесячными срочными уплатами:
где D – сумма долга, р=m число выплат и начисления процентов; n – число лет, на которые предоставлен кредит. Расчет оставшейся суммы основного долга в любой (к-й) расчетный период можно произвести по формуле:
Погашение долга равными срочными (аннуитетными) выплатамиРасходы должника при расчете по этому методу постоянны на протяжении всего срока погашения долга. Обозначим через A- сумму долга, Y - срочная уплата, Ik - проценты по займу, Rk - расходы по погашению основного долга (k - номер периода погашения). Тогда очевидно, что Y = I k + R k При этом остаток основного долга и суммы процентных платежей уменьшаются от периода к периоду, Rk- увеличиваются. Срочные уплаты являются обычными рентами. Если задан срок погашения n, то легко находим величину срочной уплаты Y. Для этого приравняем сумму долга A к современной величине ренты (см. формулу (17)). Y = A / a(n;i), (22) где a(n;i) - коэффициент приведения годовой ренты со ставкой процентаi и сроком n. Пример. Банк выдал долгосрочный кредит в сумме 4 млн. руб. на 5 лет под 6% годовых. Погашение кредита должно производиться равными ежегодными выплатами в конце каждого года, включающими погашение основного долга и процентные платежи. Проценты начисляются раз в год. Определите величину ежегодной выплаты. Решение. Здесь A = 4 млн. руб., n = 5 лет, i = 0,06. По формуле (22) находим величину ежегодной выплаты: Y = 4 Погашение потребительского кредита в финансовой математикеВ потребительском кредите проценты, как правило, начисляются на всю сумму кредита, присоединяются к основному долгу уже в момент открытия кредита. Погашение долга процентами производится частями (обычно равными суммами) на протяжении всего срока кредита. Пусть D - сумма основного долга без процентов (цена товара), n - срок кредита в годах, i - годовая ставка простых процентов, то наращенная сумма долга S равна: S=D (1+in) , а величина разового погасительного платежа R составит: R = где p - число платежей в году (обычно 12). При досрочном погашении долга возникает задача определения
остатка задолженности. Для ее решения следует разбить величину R на проценты и
сумму, идущую на погашение основного долга: R = R Один из возможных вариантов такого разбиения – равномерное
распределение выплат процентов. В этом случае вся сумма процентов делится
на равные доли по количеству выплат, и в каждом погасительном платеже проценты
составляют величину R За рубежом при определении остатка задолженности часто используется так называемое правило 78. В случае, когда срок кредита равен одному году и кредит погашается ежемесячными платежами, согласно этому правилу распределение процентных платежей по месяцам производится следующим образом:
Легко проверить, что сумма этих выплат совпадает с общей суммой процентных платежей:
(сумма номеров месяцев в году равна 78 – отсюда и название правила). Это правило можно обобщить для кредита со сроком N месяцев. При этом сумма номеров месяцев Q = N(N+1)/2 , а общая сумма начисленных процентов равна Din , где n - срок кредита в годах. Покупка в рассрочку в финансовой математикеПри покупке товара в рассрочку покупатель, по существу, реализует амортизацию долга, вызванного приобретением товара. Очевидно, что платежи рассрочки эквивалентны цене товара при некоторой норме процента. Однако, принимаемая норма процента редко когда обеспечивает эквивалентность обоих возможностей (оплата наличными или путем рассрочки). В самом деле, способ, при помощи которого определяются платежи, обычно неявно использует норму процента. Имеется два традиционно используемых способа определения платежей так, чтобы норма процента не проявлялась. Один из них называется план завышения, другой - план текущей платы. При использовании плана завышения торговец устанавливает цену товара для продажи в рассрочку и делает скидку с этой установленной цены, если товар покупается за наличные деньги. Например, набор мебели продается за 300 млн рб наличных денег. Торговец устанавливает цену 84  360 млн рб, допуская продажу за 120 млн рб наличными и выплату остатка ( 240 млн рб ) взносами по 20 млн рб в месяц в течение года. Если покупатель желает купить за наличные, ему дается скидка 16 2/3 % от установленной цены. Таким образом, ему делается скидка 60 млн рб и он заплатит за мебель 300 млн рб. Следует заметить, что завышение равно 60/300 = 20 % от цены продажи за наличные, в то время как скидка равна 60/360 = 16 2/3 % от установленной цены. Когда используется план текущей платы, дается цена товара за наличные. Платежи взносов определяются следующим образом :
При использовании одного из этих планов подлинная норма процента определяется через уравнение эквивалентности, устанавливающее, что цена продажи за наличные равна взносу наличными плюс текущая стоимость аннуитета, который образуют платежи рассрочки. То есть Наличная цена = Наличный взнос + R а п i .
85  Пусть i будет месячной нормой процента, которая обеспечивает эквивалентность этих двух возможностей. Уравнение эквивалентности с днем продажи в качестве даты сравнения дает 300 = 120 + 20 а1 2 i иа1 2 i = 9,00 . Решение уравнения такого типа ранее уже рассматривалось, поэтому мы приведем лишь результат j12 = 56,79 % . ПРИМЕР 2 Товары стоимостью 54 млн рб наличными покупаются по плану текущей платы: требуется наличный взнос 14 млн рб, после выплаты которого к стоимости добавляется 20% неоплаченного остатка и эта сумма делится на 12 равных ежемесячных взносов. Какую номинальную норму процента приm = 12 предусматривает план рассрочки? РЕШЕНИЕ После выплаты наличного взноса 14 млн рб остается неоплаченными 40 млн рб. Добавка текущей платы равна 20% от 40 млн рб или 8 млн рб. Таким образом, 48 млн рб должны быть выплачены взносами рассрочки, так что каждый ежемесячный платеж равен 4 млн рб. Две возможности приобретения товара на временной диаграмме изображаются следующим образом
Пусть i будет месячной нормой процента, которая делает эти две возможности эквивалентными. Выпишем уравнение эквивалентности с днем продажи в качестве даты сравнения
Решение этого уравнения дает результат j12 = 35,08 % . Существует много вариаций описанных планов рассрочки. Например, по одному из рекламных объявлений товары почтой продаются согласно следующему плану платежей 86 Таблица платежей (К заявке прилагается не менее 10% от стоимости товара)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 t
t
 t
t
 t
t
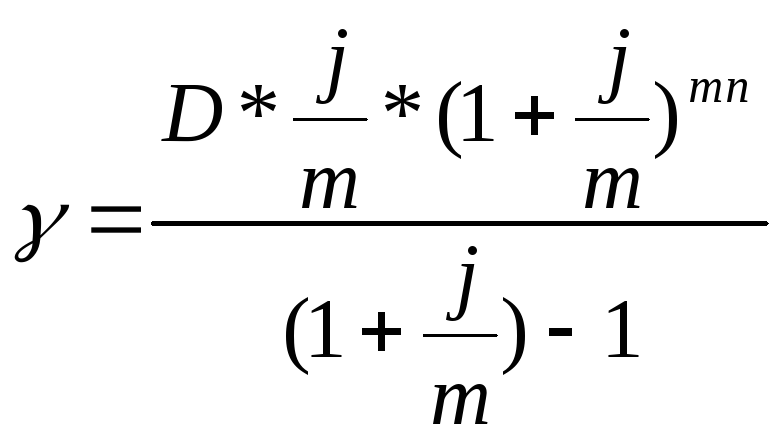 (5.8)
(5.8)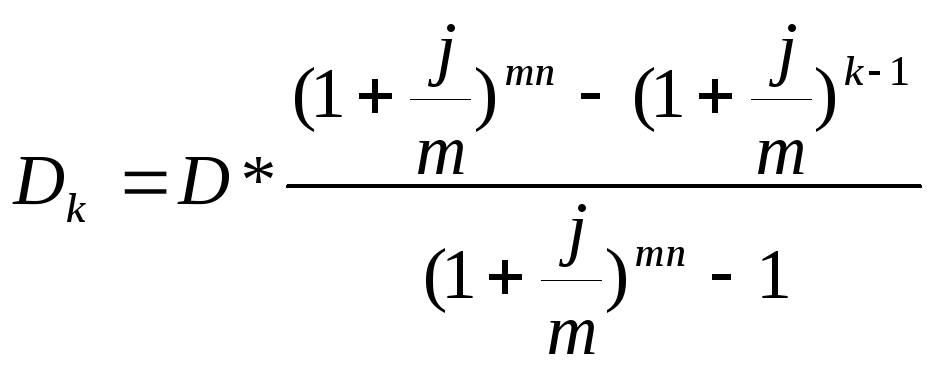 (5.9)
(5.9)