|
|
Примеры: | контрольные | курсовые | дипломные | отзывы |
|
Инфляция в оценке стоимостиВлияние инфляции на уровень доходов по вкладам в финансовой математикеПрежде всего инфляцию нужно учитывать при расчете наращенной суммы денег и при измерении реальной эффективности (доходности) финансовой операции. Рассмотрим простейшую кредитную операцию. Пусть срок действия ссуды равен Т; S0 - начальная сумма; SТ - наращенная сумма денег, измеренная по номиналу. Эта же сумма, но с учетом ее обесценения в результате инфляции, составит
Если i - годовая ставка простых процентов, Т — срок ссуды в годах, то по формуле наращения простых процентов находим:
Если же сумма S0 помещена под сложные проценты по ставке i за базовую единицу времени, и при расчете наращенной суммы SТ применяется общая схема, то реальное значение наращенной суммы с учетом инфляции вычисляется по формуле:
В частном случае, когда h - темп инфляции за базовую единицу времени, и срок ссуды Т равен целому числу n базовых единиц времени, эта формула принимает вид:
В полученных формулах величины, на которые умножается S0, представляют собой множители наращения с учетом инфляции. Реальное увеличение наращенной суммы с учетом сохранения покупательной способности денег имеет место только тогда, когда эти множители больше единицы. Для простых процентов кредитная операция приносит реальный доход, если
Таким образом, определяется минимально допустимая (барьерная) ставка i* = hT/T: при i< i* роста реальной суммы не происходит, наращение будет поглощаться инфляцией, и реальная стоимость начальной суммы S0 даже уменьшится. Это явление называется эрозией капитала. В случае сложных процентов поступают аналогично. Если, например, наращенная сумма с учетом инфляции определяется по формуле (36), то кредитная операция приносит реальный доход при условии
В этом случае минимально допустимая ставка i* = h. При i< i* операция убыточна. Годовая величина обесценивания и процентов в финансовой математикеПод годовой величиной обесценивания и процентов будем понимать стоимость, охватывающую стоимость обесценивания и процентную стоимость книжной цены. Годовая процентная стоимость вычисляется на книжную цену за этот год, то есть на книжную цену в конце предыдущего года. Хотя можно использовать для расчетов любой метод описания обесценивания, в реальной практике почти всегда используется метод погасительного фонда. Однако, норма процентов, с которой накапливает погасительный фонд, не обязательно должна совпадать с нормой, используемой для вычисления процентов на книжную цену активов. ПРИМЕР Компания выплачивает 33 млн рб за новую машину. Рассчитано, что машина будет использоваться 5 лет и что стоимость остатков после использования будет 3 млн рб. Найти годовую величину обесценивания и процентов, если для компенсации обесценивания используется погасительный фонд с нормой 4% и проценты на книжную цену вычисляются при норме 6% эффективно. 146  РЕШЕНИЕ Годовая стоимость обесценивания для этой машины вычислялась впримере параграфа 9.3. Годовая стоимость процента
для обесценивания, хотя обесценивание составляет только часть годовой величины. Формула для годовой величины и процента может быть легко
получена, когда используется метод погасительного фонда для обесценивания.
Напомним, что увеличение в погасительном в конце C -R s k 1 i . Поэтому еслиi' является годовой нормой, используемой для для вычисления процента на книжную цену, тогда полная
годовая величина в конце R(1 +i) При i = i' это выражение может быть упрощено к видуR + Ci . Доказательство этого оставим для упражнений.
интерпретировалась как величина инвестиции. 147 Индекс и темп роста инфляции в финансовой математикеИнфляция проявляется в падении реальной покупательной способности денег и общим повышением уровня цен внутри страны. Поэтому ее необходимо учитывать при проведении среднесрочных и особенно долгосрочных финансовых операций. Интенсивность инфляции измеряется числовыми показателями, характеризующими среднее изменение уровня цен для некоторого фиксированного набора (корзины) товаров и услуг за определенный период времени. Пусть выбран определенный набор товаров и услуг, и пусть за фиксированный период времени Т его стоимость изменилась от суммы Х0 до суммы ХT. Определение. Индексом инфляции (индексом цен) за период Т называется величина
а темпом инфляции за этот период называется величина
Индекс инфляции НT показывает, во сколько раз выросли цены за рассматриваемый период. Темп инфляции hT часто измеряется в процентах, при этом он показывает, на сколько процентов выросли цены за рассматриваемый период. Из определений индекса и темпа инфляции следует связь между этими показателями: НТ=1+hТ (30) Предположим, что период времени Т делится на части Т1, Т2,...,Тn, и известны индексы инфляции H1, H2,..., Hn, измеренные за эти частичные периоды. Тогда индекс инфляции НT на всем интервале времени Т равен произведению индексов инфляции на каждом из частичных интервалов Тk: НТ=Н1·Н2·...·Нn (31) Это важное соотношение иногда удобно использовать в другой форме. Пусть hk - темп инфляции на частичном интервале времени Tk, тогда Нk = 1+hk, и формулу (31) можно записать так: HT=(1+h1) (1 + h2)…(1+hk) (32) В частности, если h1 = h2 =... = hn = h , то HT = (1+h)n. Пример. Найдем индекс и темп инфляции за год, если среднемесячный темп инфляции hмес. равен 3%: Hгод = (1+hмес)12 = (1+0,03)12= 1,426; hмес =Нгод -1 = 1,426-1= 0,426 = 42,6%, Инфляционная корректировка отчетности в процессе оценки стоимости предприятия бизнесаЦелью инфляционной корректировки документации являются приведение ретроспективной информации за прошедшие периоды к сопоставимому виду; учет инфляционного изменения цен при составлении прогнозов денежных потоков и ставок дисконта. Простейшим способом корректировки является переоценка всех статей баланса по изменению курса рубля относительно курса более стабильной валюты, например американского доллара. Пример. Оборудование было приобретено в 2013 г. за 1 млн руб. ( курс рубля по отношению к доллару на дату приобретения 35 : 1). На дату оценки курс рубля к доллару составлял 36 :1, следовательно, скорректированная стоимость покупки оборудования в 2014 г. составляла: 36:35 • 1 000000 = 1 028600 руб., или 28572,2 долл. Этот способ имеет свои достоинства и недостатки. Главное достоинство - простота и возможность работы без большого объема дополнительной информации. С другой стороны, корректировка по курсу валюты дает неточные результаты в силу того, что курсовые соотношения рубля и доллара не совпадают с их реальной покупательной способностью. Более точной является переоценка статей актива и пассива баланса по колебаниям уровней товарных цен. Она может быть ориентирована как на товарную массу в целом, так и на каждый конкретный товар или товарную группу. Распространенным методом освобождения финансовой отчетности от инфляции являетсяметод учета изменения общего уровня цен. Использование данного метода позволяет абстрагироваться от материально-вещественной структуры активов предприятия и делать упор на общей оценке всего имущества с учетом покупательной способности денежной единицы и ее колебаний во времени, отражающих изменение среднего уровня цен. Этот метод заключается в том, что различные статьи финансовых отчетов рассчитываются в денежных единицах одинаковой покупательной силы (в рублях базового или текущего периода на отчетную дату). Для пересчетов используется либо индекс динамики валового национального продукта, либо индекс потребительских или оптовых цен. Универсальная формула пересчета статей баланса и финансовых отчетов в денежные единицы одинаковой покупательной силы имеет следующий вид:
Где: Вп - реальная величина статьи, скорректированной по уровню инфляции, руб.; В6 - номинальная величина статьи по данным бухгалтерского учета и отчетности, руб.; ii- индекс инфляции на момент или за период анализа; i0 - индекс инфляции в базовом периоде или на начальную дату отслеживания величины статьи баланса. Инфляционной корректировке по индексамi : iQ должны подвергаться лишь так называемые не денежные статьи: основные средства (в том числе нематериальные активы), производственные запасы, незавершенное производство, готовая продукция, малоценные и быстроизнашивающиеся предметы, обязательства, которые должны быть погашены поставкой определенных товаров и (или) оказанием определенных услуг. Напротив, денежные статьи (денежные средства, дебиторская и кредиторская задолженность, кредиты, займы, депозиты, финансовые вложения) независимо от изменения общего уровня цен инфляционной корректировке не подлежат. В данном случае речь не идет о нормализующих корректировках отчетности в процессе оценки. На практике пересчет по индексу изменения общего уровня цен осуществляется в несколько этапов. На первом - составляют финансовую отчетность в учетных ценах, т.е. с использованием первоначальных оценок. На втором - проводят классификацию всех статей отчетности на денежные и неденежные. На третьем - денежные статьи пересчитываются по текущим ценам с помощью общих индексов цен, взятых по годам приобретения активов (возникновения обязательств). Баланс по активу и пассиву достигается регулированием статьи «Нераспределенная прибыль». На четвертом этапе составляют переоцененную отчетность и рассчитывают прибыль (убыток) от изменения покупательной способности денежной единицы в отчетном периоде. Сам показатель изменения покупательной способности денежной единицы определяют с помощью общего индекса цен путем пересчета денежных активов и обязательств на начало и конец года и последующего их сравнения. Оценка не денежных активов (обязательств) в денежных единицах одинаковой покупательной силы осуществляется следующим образом. Все активы группируются по годам их приобретения (возникновения). Для каждого года стоимостная оценка группы объектов пересчитывается с использованием индексов цен текущего года и года приобретения объектов, а затем результаты суммируются. Механизм пересчета не денежных статей баланса можно выразить формулой
где Ру - оценка всех активов в денежных единицах одинаковой покупательной способности, руб.; Р iп - цена приобретения i-ro актива, руб.; i ?- общий текущий индекс цен; i ip- общий индекс цен в год приобретения i-ro объекта. Пример. Определение скорректированной величины основных средств. Оборудование было приобретено в 1975 г. за 50000 руб.; индекс цен в год приобретения - 116,3; текущий индекс цен - 339,6. Скорректированная стоимость оборудования в сопоставимых ценах составит в текущем году: 50 000-339,6: 116,3 = 146 002 руб.. Метод корректировки финансовых отчетов по изменению общего уровня цен повышает реалистичность анализа, позволяет достаточно точно установить размеры дополнительной прибыли или убытка, возникающих у предприятия в связи с изменением покупательной способности денег. Однако данный метод не учитывает разную степень изменения стоимости отдельных активов. Таким образом, анализируя внешние условия функционирования фирмы (предприятия), оценщик ставит своей целью:
Инфляция в финансовой математикеЗа три месяца стоимость условной потребительской корзины изменилась от (620+ав) рублей до (680+ ав) рублей. Определите: а) индекс потребительских цен за три месяца; б) среднемесячный индекс потребительских цен; в) темп инфляции за три месяца; г) среднемесячный темп инфляции. 5. Замена и консолидация платежей. Платежи в (6+а) тыс. руб., (4+а) тыс. руб., и (10+а) тыс.руб. должны быть погашены соответственно через 90, 165, и 270 дней. Кредитор и должник согласились заменить три платежа одним через 120 дней. Найдите величину консолидированного платежа, если используется простая процентная ставка 25% годовых и в расчет принимается простая процентная ставка. Методы учета инфляции в финансовых расчетах в финансовой математике
Владельцы денег не могут мириться с их обесцениванием в результате инфляции и предпринимают различные попытки компенсации потерь от снижения их покупательной способности. Наиболее распространенным методом является индексация ставки процентов, по которой производится наращение, поскольку:
В связи с этим вводится понятие номинальная ставка процента, т.е. ставки с поправкой на инфляцию ( i? ). Общая формула для определения простой ставки процентов, компенсирующей ожидаемую инфляцию, имеет следующий вид: i? = [(1 + n i) • J? - 1] : n где i – простая ставка процентов, характеризующая требуемую реальную доходность финансовой операции (нетто-ставка); i? – процентная ставка с поправкой на инфляцию. Пример. Банк выдал клиенту кредит на один год в размере 20 тыс. руб. по ставке 6% годовых. Уровень инфляции за год составил 18%. Определить с учетом инфляции реальную ставку процентов по кредиту, погашаемую сумму и сумму процентов за кредит. Решение: Номинальная наращенная сумма FV = PV(1 + n i) = 20'000 (1 + 0,06) = 21'200,00 руб. Номинальные начисленные проценты I = FV - PV = 21'200 - 20'000 = 1'200,00 руб. Реальная наращенная сумма FV? = FV / (1 + ? ) = 21'200 / 1,18 = 17'966,10 руб. Реальные проценты I? = FV? - PV = 17'966,10 - 20'000 = -2'033,90 руб. Таким образом, получен убыток от данной финансовой операции в размере 2'033,90 руб. Ставка по кредиту с учетом инфляции должна быть равна i? = [(1 + n i) • I? - 1] : n = (1,06 • 1,18 - 1) / 1 = 0,2508 Наращенная сумма FV = PV(1 + n i) = 20'000 (1 + 0,2508) = 25'016,00 руб. Доход банка I = FV - PV = 25'016 - 20'000 = 5'016,00 руб. Реальный доход банка I? = FV? - PV = 25'016 / 1,18 - 20'000 = 1'200,00 руб. Реальная доходность финансовой операции i = I? / PV = 1'200 / 20'000 = 0,06 Таким образом, чтобы обеспечить доходность в размере 6% годовых, ставка по кредиту с учетом инфляции должна соответствовать 25,1% годовым. Годовая ставка сложных процентов, обеспечивающая реальную доходность кредитной операции, определяется по формуле i? = i + ? + i? Пример. Определить номинальную ставку процентов для финансовой операции, если уровень эффективности должен составлять 7% годовых, а годовой уровень инфляции 22%. Решение: Процентная ставка с учетом инфляции i? = i + ? + i? = 0,07 + 0,22 + 0,07 • 0,22 = 0,3054. Таким образом, номинальная ставка составляет 30,54% при реальной ставке 7%. Для расчета номинальной ставки можно использовать следующую модель:
из которой можно сравнивать уровни процентной ставки и инфляции, проводить анализ эффективности вложений и устанавливать реальный прирост вложенного капитала. При начислении процентов несколько раз в год
Эти модели позволяют производить учет инфляции и корректировку процентных ставок. На практике довольно часто довольствуются сравнением i и ? путем вычисления реальной ставки, т.е. уменьшенной ставки доходности на уровень инфляции: i = (i - ?) / (1 + ?) Пример. Определить реальную ставку при размещении средств на год под 35% годовых, если уровень инфляции за год составляет 30%. Решение: Определяем реальную ставку: i = (0,35 - 0,2) / (1 + 0,2) = 0,125 Таким образом, реальная ставка 12,5% годовых. Модели инфляции в финансовой математике
Налоги и инфляция в финансовой математикеНалоги на полученные проценты. При начислении простых процентов
где В долгосрочных операциях при начислении налога на сложные % возможны следующие варианты: налог начисляется на весь срок сразу или последовательно в конце каждого года. В первом случае:
Во втором случае налог определяется за каждый истекший год. Сумма налогов за весь срок не зависит от метода начисления.
Инфляция. Изменение покупательской способности денег за некоторый
период измеряется с помощью индекса
Под темпом инфляции понимается относительный прирост цен за период (H), измеряется в %.
Например, если темп инфляции равен 130 % , то цены за этот период выросли в 2,3 раза. Среднегодовые темп роста цен
Поскольку инфляция является цепным процессом (цены в текущем
периоде, повышаются на
Если h - постоянный ожидаемый (или прогнозируемый) темп инфляции за период, то за n таких периодов получим:
Рассмотрим проблему обесценивания денег при их наращении. В общем случае:
При наращении по простой ставке, имеем:
Увеличение наращенной суммы с учетом сохранения покупательной
способности денег имеет место тогда, когда При наращении по сложным процентам
Если h/100 < rпроисходит малый рост. Ставка по простым процентам , которая только компенсирует инфляцию определяется по уравнению:
Для сложных процентов Ставку, превышающую Учет инфляции в финансовой математикеВ современных условиях инфляция часто играет решающую роль, и без ее учета конечные результаты представляют собой весьма условную величину. В реальной жизни инфляция проявляется в падении покупательной способности денег и общим уровнем повышения цен. Следовательно, ее необходимо учитывать при проведении финансовых операций. Рассмотрим способы ее учета. Темпы инфляции измеряются с помощью системы индексов инфляции, которые характеризуют среднее изменение уровня цен для некоторого фиксированного набора (корзины) товаров и услуг за определенный период времени. Пусть стоимость корзины в момент времени t равна S(t). Индексом цен или индексом инфляции JP за время от t1 до t2 называется безразмерная величина JP = S( t1 ) / S( t2 ), атемпом инфляции за этот период называется относительный прирост цен: h = Отсюда индекс цен JP = 1+ h. Если срок рассмотрения инфляции включает в себя n периодов, в каждом из которых средний темп инфляции равен h, то JP = (1+ h)n . В случае, когда темп инфляции в i-ом периоде равен hi , индекс инфляции за n периодов вычисляется по формуле JP = (1+ h1) (1+ h2)…(1+ hn). Индекс инфляции JP показывает во сколько раз, а темп инфляции h - на сколько процентов выросли цены за рассматриваемый период. Индекс покупательной способности денег JD равен обратной величине индекса цен: JD = 1 / J P = 1/ ( 1+ h). Пример. Вы имеете сумму в 140 тыс. руб. Известно, что за два предшествующих года цены выросли в два раза, т.е. индекс цен JP = 2. В этом случае индекс покупательной способности денег равен JD = 1/2. Значит, реальная покупательная способность 140 тыс. руб. составит в момент получения всего 140 ? 1/2 = 70 тыс. руб. в деньгах двухлетней давности. Если h - годовой темп инфляции, то годовой индекс цен равен 1 + h, поэтому наращенная сумма с учетом инфляции S и = P (
1+ i )n Очевидно, что если среднегодовой темп инфляции h равен ставке процентов i, то Sи = P, т.е. роста реальной суммы не произойдет: наращение будет поглощаться инфляцией. Если h > i , то реальная сумма меньше первоначальной. Только в ситуации h < i происходит реальный рост. Пример. Постоянный темп инфляции на уровне 10% в месяц за год приводит к росту цен в размере JP = 1,112 = 3,14. Таким образом, годовой темп инфляции h = JP - 1 = 2,14 или 214%. В целях уменьшения воздействия инфляции и компенсации потерь от снижения покупательной способности денег используется индексация процентной ставки. При этом ставка корректируется в соответствии с темпом инфляции. Скорректированная ставка называется брутто-ставкой. Вычислим эту ставку, обозначив ее через r. Если компенсируется инфляция в размере брутто-ставки при наличии простых процентов, то величину r находим из равенства множителей наращения: 1+ n? r = ( 1+ n ? i ) JP = ( 1+ n ? i )( 1+ h ) n , Отсюда
Величину брутто-ставки для наращения по сложной процентной ставке находим из равенства (n = 1): 1+ r = ( 1+ i )( 1+ h ), тогда r = i + h + h?i (15) Формулы (14), (15) означают следующее: чтобы обеспечить реальную доходность в i %, при темпе инфляции h нужно назначить ставку в размере r %. Пример. Банк выдал на 6 месяцев кредит - 5 млн руб. Ожидаемый месячный уровень инфляции – 2 %, требуемая реальная доходность операции равна 10 % годовых. Определите ставку процентов по кредиту с учетом инфляции, размер наращенной суммы и величину процентного платежа. Решение. Индекс инфляции JP = (1 + 0,02)6 = 1,1262. Из (14) получим величину брутто-ставки: r = Размер наращенной суммы S= P(1+ n r ) = 5 (1 + 0,5?0,365 ) = 5,9126 млн. руб. Величина процентного платежа ( плата за кредит ) I = 5,9126 - 5,0 = 0,9126 млн. руб. Пример. Кредит в 1 млн. руб. выдан на два года. Реальная доходность должна составлять 11% годовых (сложные проценты). Расчетный уровень инфляции 16% в год. Определите ставку процента при выдаче кредита, а также наращенную сумму. Решение. Из формулы (15) имеем: r = 0,11+0,16+ 0,11? 0,16 = 0,2876; S = 1,0 ( 1 + 0,2876 )2 = 1,658 млн. руб. Задачи 4.1. Кредит 500 тыс. руб. выдается с 20.06.98г. по 15.09.98г. При выдаче кредита считается, что индекс цен к моменту его погашения составит 1,3. Определите брутто-ставку и погашаемую сумму. Ответ: R = 134% ; S R = 658 194 руб. 4.2. Кредит в размере 5 млн руб. выдается на 3 года. Реальная доходность операции должна составлять 3 % годовых по сложной ставке. Расчетный уровень инфляции составляет 10% в год. Вычислите брутто-ставку и погашаемую сумму. Ответ: R = 13,3 % ; SкR = 7 272 098 руб. 4.3. В банк помещен вклад в сумме 100 тыс. руб. под 100 % годовых сроком на 5 лет. Ожидаемый в течение этого периода темп инфляцииh = =50 % в год. Определите реальную сумму, которую будет иметь клиент по истечении пяти лет: а) с учетом инфляции; б) без учета инфляции. 4.4. Какую ставку должен назначить банк, чтобы при годовой инфляции 11% реальная доходность оказалась 6 %. Список литературы и источников на тему "Инфляция в оценке стоимости"
 Полный комплект решенных тестов и практикумов по оценке для курсов оценщиков умц Полный комплект решенных тестов и практикумов по оценке для курсов оценщиков умцДругие похожие работы |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
© 2002 - 2024 RefMag.ru |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
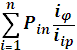
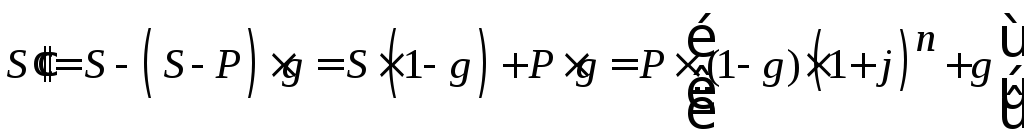 , (50)
, (50)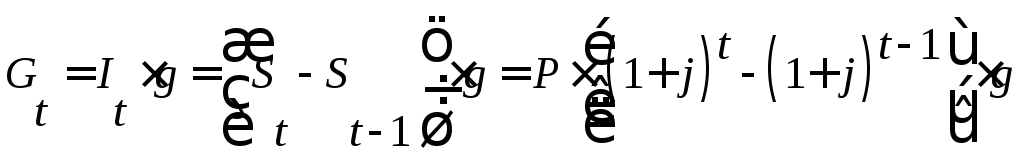 , (51)
, (51)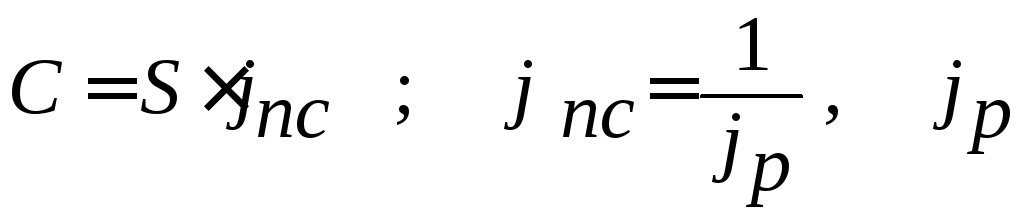 - индекс цен.
- индекс цен.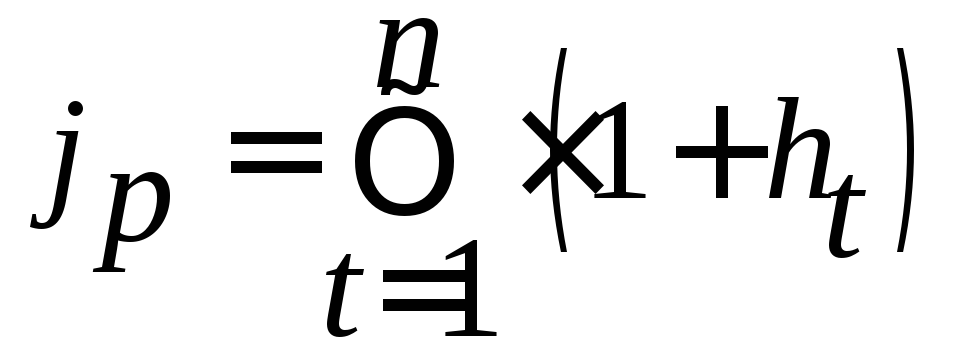 ;
(52)
;
(52)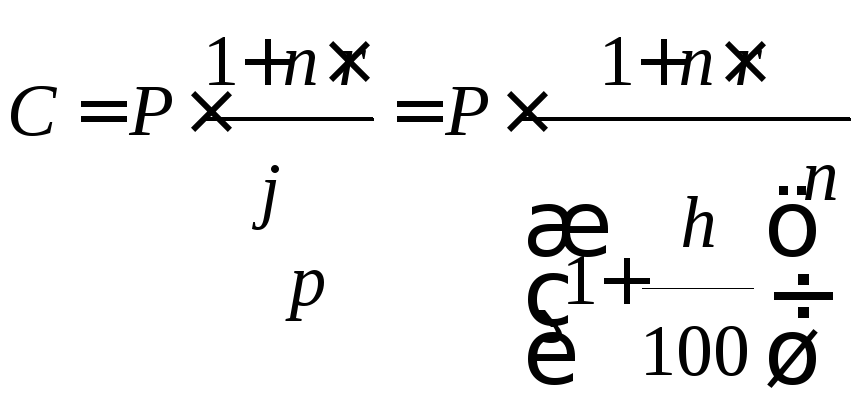 , (55)
, (55)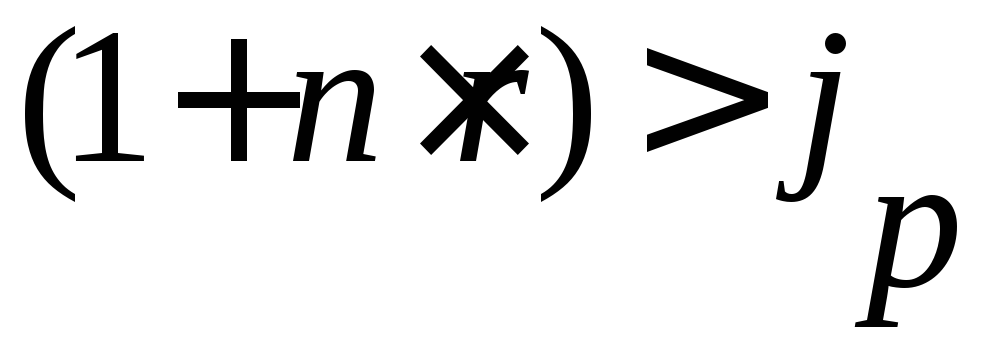 .
.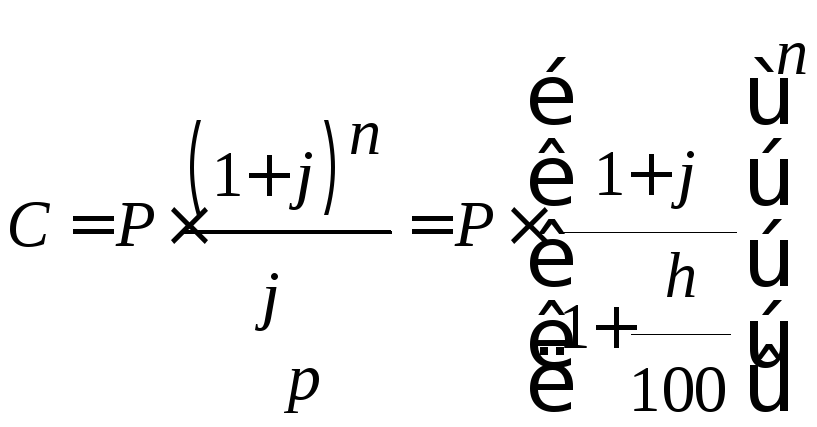 , (56)
, (56)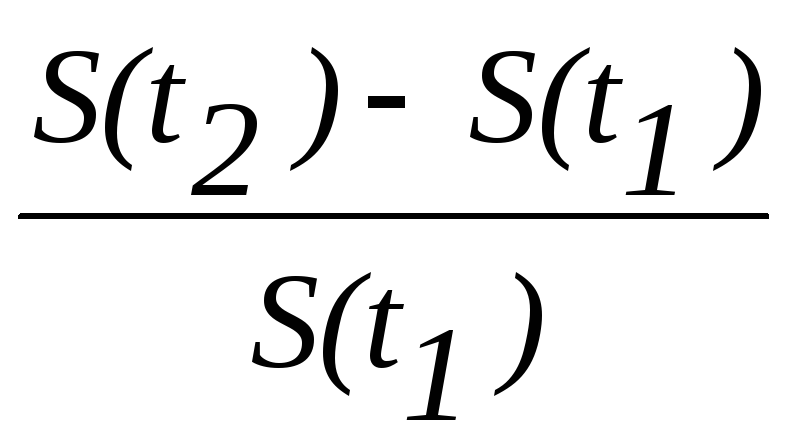 =JP
- 1.
=JP
- 1.