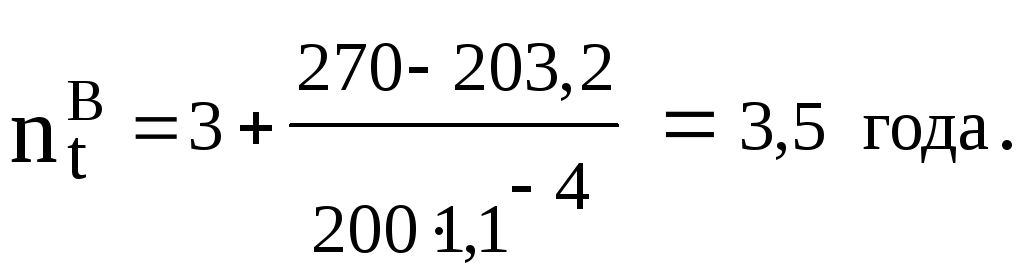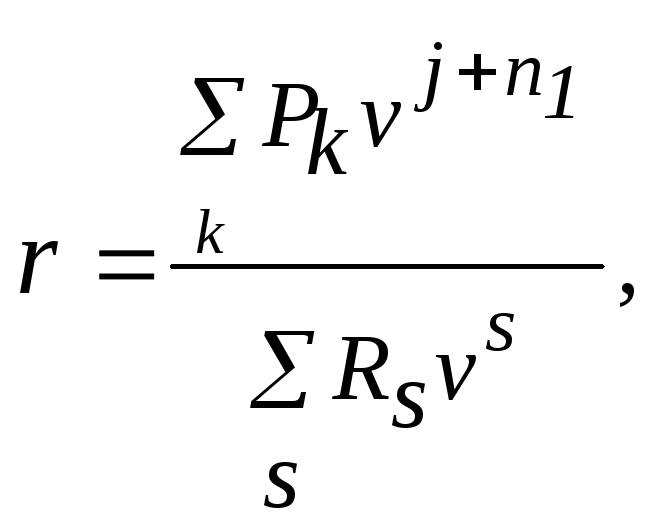|
|
Примеры: | контрольные | курсовые | дипломные | отзывы |
|
Эффективность и оценка стоимостиПоказатели эффективности инвестицийВинвестиционном процессе имеется два потока: потока инвестиций и последовательное получение дохода. Эти два потока могут следовать один за другим, между ними может быть некоторый разрыв или наложение во времени. При изучении эффективности инвестиций оба эти потока могут рассматриваться и сопоставляться по отдельности или как одна последовательность. В последнем случае инвестиционные расходы включаются в поток с отрицательным знаком. Под чистым доходом понимают общий доход (выручку), полученный в каждом временном отрезке, за вычетом всех платежей, связанных с его созданием и получением. Вэти платежи входят прямые и косвенные расходы по оплате труда и материалов, налоги. Элемент объединенного потока инвестиций и доходов в момент t определяется следующим образом: Rt=(Gt-Ct)-( где Rt - элемент потока наличности, Gt –
ожидаемый Ct – общие текущие расходы, прямые и косвенные (амортизационные отчисления сюда не включаются), Dt – расходы, на которые распространяются налоговые льготы,T – налоговая ставка, Kt – инвестиционные расходы, St – различные виды компенсаций, дотаций. Анализ производственных инвестиций в основном заключается в оценке и сравнении эффективности альтернативных инвестиционных проектов. В качестве измерителей обычно используются характеристики, основанные на дисконтировании потоков ожидаемых поступлений и расходов и приведении их к одному моменту времени. Ставку, по которой производится дисконтирование, называют ставкой сравнения. При выборе ставки сравнения ориентируются на существующий или ожидаемый уровень ссудного процента и корректируют ее с учетом ожидаемого риска. Ясно, что будущая ставка является не вполне определенной величиной, поэтому расчеты носят условный характер и могут выполняться не для одного, а для нескольких значений ставки. В финансовом анализе обычно применяют четыре показателя эффективности инвестиций: 1.чистый
приведенный доход (ЧПД, 2.срок окупаемости (payback period), 3.внутренняя норма доходности (Internal Rate of Return – IRR), 4.индекс рентабельности (profitability index PI). Чистый приведенный доход Этот показатель часто считается основным. Будем обозначать его как NPV. Эта величина характеризует конечный абсолютный результат, рассчитываемый как разность дисконтированных на один момент времени показателей дохода и капиталовложений, то есть NPV = ?Rt vt , где Rt – член потока платежей (объединенного потока инвестиций и доходов),v – дисконтный множитель,v=1/(1+q), гдеq – ставка сравнения. 60  АНАЛИЗ ФИНАНСОВЫХ ПОТОКОВ Если инвестиции и доходы равномерные и дискретные, то W можно найти как разность современных величин двух рент (одной, представляющей инвестиции, и другой, отсроченной до начала периода отдачи, представляющей поток доходов). Несмотря на то, что этот показатель чистого приведенного дохода является основой для определения других измерителей эффективности, у него есть ряд существенных недостатков. Один недостаток его состоит в том, что он предполагает известными все будущие члены потока, что на практике нереально. Кроме того, являясь абсолютным показателем, он не дает представления об относительной эффективности вложения финансовых средств. Срок окупаемости Под сроком окупаемости в финансовом анализе понимают продолжительность периода, в течение которого сумма чистых доходов, дисконтированных на момент завершения инвестиций, равна сумме приведенных на этот же момент инвестиций. Если приведенная сумма инвестиций составляет K, а доход поступает в конце каждого года, то расчет срока окупаемости сводится к тому, что сначала определяется сумма m Sm= ?Rtvt , t=1 удовлетворяющая условию Sm<K<Sm+1. Срок окупаемости равенm лет плюс некоторая доля (m+1) – го года, примерно равная K ? Sm . Rm+1vm+1 Если поток доходов представляет собой ренту, то срок окупаемости находится путем приравнивания капиталовложений современной величине финансовой ренты, представляющей доходы, и решения этого уравнения относительно срока n. Основной недостаток этого показателя в том, что он не учитывает доходы, поступающие за пределами срока окупаемости. Внутренняя норма доходности Под внутренней нормой доходности (IRR) понимают ту расчетную ставку процентов, применение
которой к инвестициям порождает данный поток доходов. Чем выше эта ставка (мы ее
будем обозначатьIRR), тем больше эффективность
капитальных вложений. Если капиталовложения осуществляются только за счет
привлеченных средств, причем кредит получен по ставкеi, то разность Внутренняя норма доходности IRR определяется в общем случае путем решения уравнения ?Rt vt = 0 , t где v=1/(1+IRR), Rt – член объединенного потока инвестиций и доходов. Уравнение имеет нелинейный вид и решается итеративно методом линейной интерполяции или другими приближенными методами. За рубежом расчет внутренней нормы доходности часто
применяют в качестве первого шага количественной оценки эффективности
капиталовложений. Для дальнейшего анализа отбираюттеинвестиционныепроекты,
61 Анализ эффективности инвестиционных процессов - финансовая математикаВ условиях рыночной экономики инвестирование позволяет нарастить капитал. Для этого надо уметь анализировать инвестиционные процессы. В инвестиционном проекте средства сначала вкладываются в какую-либо сферу (производство, строительство, торговля, ценные бумаги и т.д.) а затем они постепенно возвращаются, принося инвестору к концу срока проекта определенную прибыль. Задача инвестора: на основе имеющихся на момент начала проекта данных о доходности вложений в различные сектора рынка и их прогнозе на период реализации проекта выбрать оптимальный вариант вложения имеющихся у него финансовых средств. Хотя такая задача сложна и содержит в себе моменты неопределенности и риска, но даже простые модели позволяют многое прояснить, выяснить связи между параметрами инвестиционных процессов, допустимые диапазоны их изменения и т.д. и, в конечном счете, принять правильное решение. Непосредственным объектом анализа инвестиционных процессов являются потоки платежей, в которых инвестиции отрицательны, доходы положительны. Показатели эффективности инвестиций - финансовая математикаМетоды, которыми осуществляют оценку эффективности инвестиционного процесса, основаны на приведении финансовых потоков инвестиций к одному моменту времени, следовательно, важным моментом является выбор ставки сравнения, по которой производится дисконтирование. Какую ставку принять в данной ситуации - дело макроэкономического анализа и прогноза. В общем случае для решения таких задач применим и стохастический анализ и экономико-математическое моделирование. Для выбора вариантов инвестиционного проекта (ИП) применяемые методики чаще всего основаны на использовании четырех показателей:
Каким образом вычисляется первый показатель, мы уже рассмотрели в предыдущем пункте. Отрицательное значение NPV говорит о нецелесообразности для инвестора данного варианта ИП. Среди вариантов с NPV?0 выбирают тот, у которого NPV больше. Однако этот лучший с точки зрения NPV проект надо еще сравнить с вариантом вложения средств на банковский депозит, учитывая, что риск в этом случае меньше. Рассмотрим пример, для которого последовательно вычислим все показатели эффективности ИП. Пример (основной). Даны два варианта ИП А и Б, которые характеризуются следующими потоками платежей (все показатели отнесены на конец года) (см. рис. 8): СА = (-100; -150; 50; 150; 200; 200), СБ = (-200; -50; 50; 100; 100; 200). Р Первый показатель у каждого потока отнесен к первому году, следующий ко второму и т.д. При ставке сравнения i = 10% получим: NPVА = 162,2; NPVБ = 57,7. Следующий показатель - срок окупаемости (nок). Это срок, за который можно возвратить инвестированные в проект деньги. Рассмотрим определение срока окупаемости без учета фактора времени. В этом случае nок находимпоследовательным суммированием доходов и подсчетом времени до тех пор, пока сумма дохода не окажется равной сумме инвестиций. Пример. Сравним по сроку окупаемости nок два варианта ИП из основного примера. Для варианта А суммируем годовые доходы: 50 + 150 + 200x = 250, x = 0,25 года. Отсюда, для варианта А имеем nок = 2 + 0,25 = 2,25 года. Аналогично для варианта Б находим: 50 + 100 + 100 = 250, следовательно, nок = 3 года. С финансовых позиций более обоснованными являются методы расчета срока окупаемости, учитывающие фактор времени. Рассмотрим простейший из них. Более сложные методы см. в [1]. Представим данный метод в виде алгоритма.
Тогда m - целое число лет, составляющих срок окупаемости nt. Доля года рассчитывается по формуле (К- Рm)/Rm+1Vm+1.
nt = m + (К- Рm)/Rm+1Vm+1. Оценим nt для предыдущего примера. Здесь t = 2 - момент завершения инвестиций, ставка сравнения i = 10 %. Вариант А: сумма инвестиций, приведенная на момент их завершения КА = 100(1+0,1) +150 = 260. Далее, Р2 = 169,4; Р3 = 319,7 т.е. Р2 ? КА ? Р3. Следовательно, m = 2 годам, тогда
Аналогично для варианта В: КВ = 200(1+0,1) +50 = 270, Р3 = 203,2; Р4 = 339,8 т.е. Р3 ? КВ ? Р4, тогда m = 3 годам и окончательно:
Основной недостаток срока окупаемости в том, что он не учитывает доходы после момента полного возмещения вложенных средств. Особенно нагляден этот недостаток в случае, когда отдачи от вложений капитала неравные. Поэтому срок окупаемости не должен служить критерием выбора инвестиционного проекта, а использоваться в виде ограничения при принятии решения о данном инвестиционном проекте. Внутренняя норма доходности. Найдем такую ставку процента iB, при которой становятся равными дисконтированная стоимость потоков расходов и дисконтированная стоимость потока доходов. Проведем финансовый анализ для инвестора, т.е. будем считать его расходы отрицательными, поступления положительными. Если обозначить члены финансового потока через RS (RS ? 0 - расходы, RS ? 0 - доходы), то iB определится из уравнения
Если уравнение NPV(i)=0 имеет единственный положительный корень iB, то его называют ставкой доходности или внутренней нормой доходности (internal rate of return = irr) инвестиционного проекта. Эта норма доходности представляет собой максимальную ставку процента, под которую инвестор мог бы взять кредит для финансирования ИП, а доходы, поступающие от реализации проекта, использовались бы для погашения суммы кредитов и процентов. Пусть кредит получен по ставке, тогда при i = iB положение инвестора не изменится при принятии такого проекта (бесприбыльный проект). Если i ? iB ,то такой ИП нужно отвергнуть. При i ? iB проект можно принять, выбрав из всех вариантов проект с наибольшим значением iB. Таким образом, экономическая задача свелась к решению математической задачи отыскания корней уравнения NPV(i)=0. Здесь уместно сделать следующее замечание относительно существования и единственности положительного корня уравнения (1). В [2] сформулирована теорема, утверждающая, что если последовательность (R(1), R(2),…, R(n )), где R(k)= R1+R2+…+Rk - сумма накопленных платежей до момента tk, причем, R0 ?0 и R(n) ? 0, имеет ровно одну перемену знака, то уравнение (30) имеет единственный положительный корень. На практике вначале проверяют выполнения условия теоремы, и если оно выполнено, то с помощью компьютера находят корень уравнения (30). Однако этот корень можно вычислить с помощью линейной интерполяции. Именно, если f(a) и f(b) имеют разные знаки, например, f(a) ? 0, f(b) ? 0, то приближенное значение корня можно вычислить по формуле
Пример. Пусть некоторому ИП соответствует следующий поток платежей: Rk = (-5, 1, -3, 8, 4) при tk = (0, 1, 2, 3, 4). Найдем iB. Решение. Проверим условие теоремы. Rk= (-5, -4, -7, 1, 5), т.е. последовательность {Rk}имеет ровно одну перемену знака. Следовательно, уравнение f(i) = -5 + (1+i)-1 –3(1+i)-2 + 8 (1+i)-3 + 4(1+i)-4 = 0 имеет единственный положительный корень iB. Составляя таблицу значений f(i) от 0,20 до 0,25 с шагом 0,01, заметим, что f(0,22) ? 0, f(0,23) ? 0 т.е. iB?(0,22; 0,23). Используя формулу линейной интерполяции с шагом 0,01, получим:
Следовательно, внутренняя норма доходности данного ИП iB = 22.11 %. Последний из рассматриваемых показателей эффективности – индекс рентабельности (рентабельность) r ИП представляет собой отношение суммы всех дисконтированных денежных доходов от инвестиций к сумме всех дисконтированных инвестиционных расходов:
где Pk - показатели чистого дохода в момент времени tk, Rk - размеры инвестиционных затрат, S = 1,2,3,…n1; j = 1,2,…n2, где n1 – продолжительность процесса инвестиций, n2 – продолжительность периода отдачи от инвестиций. Если r ? 1, то проект должен быть отклонен. Среди проектов, у которых r ? 1, следует отдать предпочтение проекту с наибольшим индексом рентабельности. Заметим, что не всегда проект с наибольшим r будет иметь и самую большую NPV. Пример. Вычислим рентабельность для ИП из основного примера (ставка процента i = 10 %). Имеем:
В заключение сделаем некоторые замечания о методике выбора ИП на основе рассмотренных четырех показателей эффективности. Если для фирмы важен, например, период окупаемости, тогда сначала на его основе отвергают неприемлемые варианты. Если же этот показатель для фирмы не очень важен, то его не применяют вообще. Как было показано выше, все показатели эффективности строятся на основе дисконтирования инвестиционного потока, поэтому результаты сравнения зависят от выбора важнейшего параметра анализа – принятой ставки сравнения. Действительно, если в последнем примере ставка сравнения равна 20 %, тоrA= 1,105, rB = 0,763. Это объясняет тот факт, почему многие фирмы применяют не один, а два и более показателей эффективности. Наибольшей популярностью у инвесторов пользуется внутренняя норма доходности, которая считается основным критерием, а остальные – дополнительными. В странах с развитой рыночной экономикой большинство крупных фирм в качестве пары «основной - дополнительный критерий» используют чаще всего пару «iB- NPV» и «NPV - iB» . Если при выборе ИП с помощью выбранной пары возникают заметные расхождения, то привлекают третий показатель, или проводят более глубокий финансовый анализ (см. [ 6 ]). Для окончательного решения привлекаются и дополнительные критерии, связанные, например, с экологией и безопасностью персонала. Задачи 8.1. Инвестор вкладывает 10 денежных единиц (д.е.) в момент t = 0, затем 4 д.е. через 2 года и получает 20 д.е. через 5 лет. Найдите NPV, iB для этого проекта, если i = 10%. 8.2. ИП характеризуется следующим потоком платежей: R = (-80, 10, 10, 20, 40, 30, 50), t = (0, 1, 2, 3, 4, 5, 6). Определите PV доходов, срок окупаемости nок (без учета фактора времени), если i = 10%. 8.3. Для финансового потока R = (-90, 10, 20, 30, 30, 40, 50), t = (0, 1, 2, 3, 4, 5, 6) определите NPV , (i = 10%). 8.4. Фирме предоставляется возможность инвестировать 1000$ за доход в 500, 1000 и 200$ в конце первого, второго и третьего года соответственно в рамках проекта, срок которого три года. Фирма может кредитовать и заимствовать под 5 % годовых. Выгоден ли такой проект фирме с точки зрения NPV, если i = 10%? Ответ: NPV = 556$. 8.5. Вычислите индекс рентабельности двух ИП А и Б, каждый из которых требует единовременных затрат в размере 500 д.е. и 800 д.е. соответственно. Доходы ожидаются в конце года для проекта А в размере 715 д.е., для проекта Б – 1100 д.е. Ставка дисконта 10%. Ответ: RA = 1,3; RB = 1,25. 8.6. Найдите NPVA и NPVB для инвестиционных проектов из предыдущей задачи. 8.7. Для основного примера вычислить iB., если i = 10% Ответ: A: f(0,31) ? 0, f(0,33) ? 0, iB = 31,2 %; Б: f(0,16) ? 0, f(0,18) ? 0, iB = 17,1 %. Портфель минимального риска при заданной эффективности в финансовой математикеДан портфель из трех ценных бумаг с доходностями µ1= (10+а)%; µ2= (15+а)%; µ3= (21+а)% и ковариационной матрицей
1+а) -1 0 -1 (9+а) -2 0 -2 (4+а) Найти портфель минимального риска с доходностью µ = 25% и его риск. Написать уравнение минимальной границы. Литература. 1. Боди З., Мертон Р. Финансы. Пер. с англ. М. :Издательский дом “Вильямс”, 2008. 2. Ширяев А.Н. Основы стохастической финансовой математики. Т1,2 М.: ФАЗИС, 1998. 3. Четыркин Е.М. Финансовая математика. М.: Дело, 2001. 4. Малыхин В.И. Финансовая математика. М.: ЮНИТИ-ДАНА, 2000. 5. Винстон У.Л. MicrosoftExcel: анализ данных и построение бизнес моделей. Пер. с анг. М.: Издательско - торговый дом “Русская редакция”, 2005. 6. Ковалев В.В. Финансовый менеджмент: теория и практика.3-е изд. М.:ТК Велби Проспект, 2010 Условия задач на эффективность инвестиций1) Имеются два инвестиционных проекта, в котором потоки платежей (поступление с учетом капиталовложений) на конец года характеризуются следующими данными:
Сравнить проекты по величине чистого приведенного дохода, если норматив доходности (ставка сравнения) принята на уровне 10%. Определить сроки окупаемости. 2) Проект предлагается реализовать за три года. Планируются следующие размеры и сроки инвестиций: в начале 1го года единовременные 5 млн. руб., во 2м году только равномерные расходы – 10 млн. руб., в конце 3го года единовременные затраты – 3 млн. руб. Отдачу планируют получать 15 лет: в первые 3 года по 2 млн. руб., далее в течение 10 лет ежегодно по 6 млн. руб., в оставшиеся 3 года по 3 млн. руб. Доходы поступают равномерно в пределах годовых интервалов. Ставка проведения - 5%. Окупятся ли капиталовложения? 3) Определить значение процентной ставки для проекта, рассчитанного на 3 года, требующего инвестиции в размере 30 млн. руб. и имеющего предполагаемые денежные поступления в размере 4, 10, 15 млн. руб. 4) Определить индекс доходности (рентабельности) по данным задач 1 и 2. 5) Инвестор вкладывает капитал в проект рассчитанный на 4 года при уровне налогообложения и инфляции на уровне 10% в год, рассчитывая на следующие ежегодные денежные потоки: выручка 2500 тыс. руб.; текущие затраты 1500 тыс. руб., амортизация 700 тыс. руб. Определить чистые денежные потоки для инвестора. Список литературы и источников на тему "Эффективность и оценка стоимости"
Другие похожие работы
|
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
|
© 2002 - 2024 RefMag.ru |
|||||||||||||||||||||||||||||
|
|
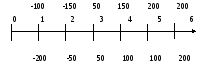 ис. 8
ис. 8