|
|
Примеры: | контрольные | курсовые | дипломные | отзывы |
|
Дисконтирование в оценке стоимостиДисконтирование и его использование
Дисконтирование и ее сущность
Дисконтирование и финансовая математикаПри дисконтировании решается задача, обратная вычислению
наращенной суммы, т.е. по заданной заранее наращенной сумме S
определить, какую сумму P надо инвестировать, чтобы через
время t при постоянной ставке простого процента i
получить сумму S. Из формулы (2) следует, что с будущей суммы S. Операция вычисления современной стоимости
будущей суммы денег называется математическим дисконтированием, а
величина дисконтирующим множителем. Разность D = S - P называют дисконтом суммы. Пример. Заемщик получил кредит на 6 месяцев под 20 % годовых с условием вернуть 300 тыс. руб. Какую сумму получил заемщик в момент заключения договора? Решение. Принимая год равным 360 дням, а 6 месяцев - 180 дням, получим S = 300 /( 1 + 0,20 ? 180/360 ) = 272,73 тыс. руб.; Пример. Какую сумму инвестор должен внести сегодня под простые проценты по ставке 50 % годовых, чтобы накопить 100 тыс. руб.: а) за полгода; б) за два года. Решение. Имеем ( в рублях) : а) S = 100 000 / (1 + 0,5 ? 0,5) = 80 000; б) S = 100 000 / (1 + 0,5 ? 2) = 50 000. Второй вид дисконтирования называется банковским учетом. Суть его в следующем. Банк приобретает вексель у вкладчика до наступления срока платежа по цене, которая меньше суммы, указанной на векселе, т.е. учитывает вексель сдисконтом (скидкой). При учете векселя применяется банковский учет. Для этого банк вводит учетную ставку d . Размер дисконта D = S? n ? d, где d - годовая учетная ставка, n - срок от момента учета до даты погашения векселя в годах. Сумма, которую получит вкладчик при учете векселя, равна P = S – S ? n ? d = S ( 1 - n ? d). Учет производится по банковскому правилу, т. е. К = 360 (число дней ссуды точное). Соотношение между учетной ставкой банка d и процентной ставкой i за один период следующее:
Пример. Тратта (переводной вексель) выдан на сумму 100 тыс. руб. с уплатой 18 ноября. Владелец векселя учел его в банке 24 сентября по учетной ставке 20%. Определите сумму, полученную при учете. Решение. Срок от момента учета до даты погашения равен 55 дням. Тогда искомая сумма равна: P = S (1 - n ? d ) = 100 000 ( 1 - 55/360 ? 0,2 ) = 96 944,4 руб. Дисконт составит 100 000 - 96 944,4 = 3 055,6 руб. Задачи 2.1. Вексель, выданный на сумму 15 000 руб. с уплатой через 100 дней, с условием начисления простых процентов по ставке 10 % годовых, был учтен в банке за 50 дней до наступления срока по простой учетной ставке 15%. Определите полученную владельцем сумму при учете векселя и величину дисконта, полученную банком. 2.2. Владелец векселя в 100 тыс. руб. со сроком погашения 5 мес. учитывает его в банке спустя два месяца. Банк учитывает вексель за 94 тыс. руб. Определите дисконт D, d3 - учетную ставку банка за 3 месяца, годовую учетную ставку d и учетную стоимость векселя за месяц до погашения. Ответ: D = 2 тыс. руб.; d3 = 0,06; d = 0,24 ; P = 98 тыс. руб. 2.3. Вексель выписан 10 января 1998 года с датой погашения 10 октября 1998 года. Проценты по векселю начисляются по ставке 12 % в год. Определите учетную (выкупную) стоимость векселя, если вексель учтен в банке 10 мая 1998 года по учетной ставке 10 %. Ответ: 104,422 тыс. руб. 2.4. Выведите соотношение (7). Дисконтирование по сложной учетной ставке в финансовой математикеВ практике учетных операций иногда применяют сложную учетную ставку. В этих случаях процесс дисконтирования происходит с замедлением, так как каждый раз учетная ставка применяется к сумме, уже дисконтированной на предыдущем шаге по времени. По аналогии с наращением по сложным процентам ST=S0·(1+i)Т дисконтирование по сложной годовой учетной ставке d осуществляется по формуле S0=ST·(1-d)Т (44) Дисконтный множитель этом равен (1 - d)T. Сравним дисконтирование по сложной учетной ставке d с дисконтированием по такой же простой учетной ставке. Возьмем для иллюстрации d = 40% и вычислим для различных значений срока операции Т дисконтные множители для сложной ставки kсл(T) = (1-d)T и для простой ставки kпр(T) = (1-d T). Результаты приведены ниже в таблице.
Видно, что значение множителя kпр(T) равномерно убывает с ростом T, обращается в ноль при Т = 2,5 года и является отрицательным при T> 2,5 (то есть, при Т > 2,5 кредитная операция не имеет смысла). Множитель kсл (T) тоже убывает с ростом Т, но остается положительным при всех T>0. По аналогии с номинальной и эффективной ставкой процентов вводятся понятия номинальной и эффективной учетных ставок. Определение. Годовая учетная ставка f называется номинальной, если дисконтирование производится m раз в год по ставке f/m. Приведенная сумма S0 при этом вычисляется по формуле S0 = ST·(1- f/m)mТ (45) где Т срок ссуды. Дисконтный множитель равен (1-f/m)mT. Определение. Эффективная учетная ставка - это годовая учетная ставка, дающая тот же результат, что и m -кратное дисконтирование по ставке f/m. Обозначим эффективную учетную ставку через d. По определению дисконтные множители по двум видам ставок (эффективной и номинальной) должны совпадать: (1-d) =(1- f/m)m Отсюда получаем формулу для расчета эффективной учетной ставки по заданной номинальной: d=1-(1-f/m)m (46) Ключевые параметры процесса дисконтирования в финансовой математикеПериод времени Процентная ставка \ Ставка дисконтирования Ожидаемая величина будущих денежных потоков Текущая стоимость будущих денежных потоков Если известны любые три из перечисленных выше параметров, может быть определен неизвестный четвертый. Обычно, от Оценщика требуется определение текущей стоимости будущих денежных потоков и/или процентной ставки \ ставки дисконтирования.
 Операции наращивания и дисконтирования в финансовой математикеСтоимость определенной суммы денег это функция от времени возникновения денежных доходов или расходов. Тезис «время-деньги» всем хорошо известен. Временная стоимость денег обусловлена двумя факторами:
П Этот показатель рассчитывается отношением приращения исходной суммы к базовой величине, в качестве которой можно брать либо PV либо FV. Таким образом, ставка рассчитывается по одной из двух формул. Темпы прироста
Темпы снижения
В финансовых вычислениях первый показатель называется:
Второй показатель называется:
Обе ставки взаимосвязаны:
Оба показателя могут выражаться либо в долях единицы, либо в процентах. Очевидно, что
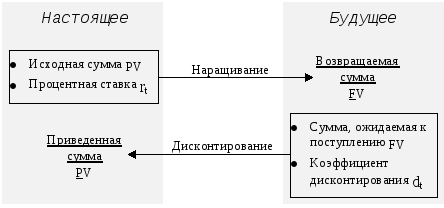
В любой простейшей финансовой сделке всегда присутствуют три величины, из которых две заданы, а одна является искомой. Если заданы исходная сумма PV и процентная ставка Если заданы сумма, ожидаемая к получению в будущем (возвращаемая сумма) FV и
ставка дисконта
Рис.1. Логика финансовых операций. В качестве коэффициента дисконтирования может использоваться либо процентная ставка (математическое дисконтирование), либо учетная ставка (банковское дисконтирование). Из формулы (1) следует:
и Выводы:
Операция дисконтирования в финансовой математикеВ финансовой практике часто возникает задача, обратная задаче наращения процентов: требуется определить, какую сумму S0 нужно вложить при заданной ставке простых или сложных процентов i, чтобы через определенный срок Т лет получить желаемую сумму ST. Процесс вычисления неизвестного S0 по известному ST называется дисконтированием или приведением. Сумма S0 называется современным или приведенным значением для ST, а разность D = ST - S0 называют дисконтом суммы ST. В зависимости от вида процентной ставки применяют два метода дисконтирования: математическое дисконтирование и банковский учет. В первом случае используется ставка наращения, во втором - учетная ставка. Математическое дисконтирование представляет собой формальное решение задачи, обратной наращению первоначальной суммы ссуды. В случае простых процентов наращенная за Т лет сумма SТ вычисляется по формуле: ST=S0·(1+i T) где i - годовая процентная ставка. Отсюда находим
Дробь 1/(1 + i·T) называют дисконтным множителем. Для краткосрочных ссуд в формуле (39) нужно положить T = ?/ K, где ? - срок, измеряемый в днях, К - число дней в году. В случае сложных процентов наращенная сумма вычисляется по формуле: ST=S0·(1+i)T Отсюда находим
так что дисконтный множитель равен 1/(1+i)T. Если начисление сложных процентов производится m раз в году по годовой номинальной ставке j, то наращенную сумму находят по формуле: SТ = S0·(1+ j/m)mТ откуда получаем:
Дисконтный множитель здесь равен 1/(1+j/m)mТ. Формулы (39)-(41) - это основные формулы математического дисконтирования. Они связывают между собой современное S0 и будущее SТ значения сумм. Ретроспективный анализ и прогноз валовой выручки от реализации при оценке стоимости бизнеса в методе дисконтированных денежных потоковНеобходим учет следующих факторов: - номенклатура выпускаемой продукции; - объемы производства и цены на продукцию; - ретроспективные темпы роста предприятия; - спрос на продукцию; - темпы инфляции; - имеющиеся производственные мощности; - перспективы и возможные последствия капитальных вложений; - общая ситуация в экономике, определяющая перспективы спроса; - ситуация в конкретной отрасли с учетом существующего уровня конкуренции; - доля оцениваемого предприятия на рынке; - долгосрочные темпы роста в послепрогнозый период; - планы менеджеров данного предприятия. Правило: прогноз валовой выручки основывается на ретроспективных показателях и прогнозируется с учетом возможных темпов роста предприятия и отрасли в целом. - бизнес-план предприятия (анализ планов предприятия по сохранению или увеличению доли на рынке); - анализ позиций основных конкурентов. Список литературы и источников на тему "Дисконтирование в оценке стоимости"
 Полный комплект решенных тестов и практикумов по оценке для курсов оценщиков умц Полный комплект решенных тестов и практикумов по оценке для курсов оценщиков умцДругие похожие работы |
||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
|
© 2002 - 2024 RefMag.ru |
||||||||||||||||||||||||||||
|
|
 ростейшим видом финансовой сделки является однократное представление
в долг некоторой суммыPV (present value) с условием, что через какое-то время t
будет возвращена большая сумма FV (future value). Результат такой сделки
оценивается с помощью специального коэффициента, который называется
ставкой.
ростейшим видом финансовой сделки является однократное представление
в долг некоторой суммыPV (present value) с условием, что через какое-то время t
будет возвращена большая сумма FV (future value). Результат такой сделки
оценивается с помощью специального коэффициента, который называется
ставкой.