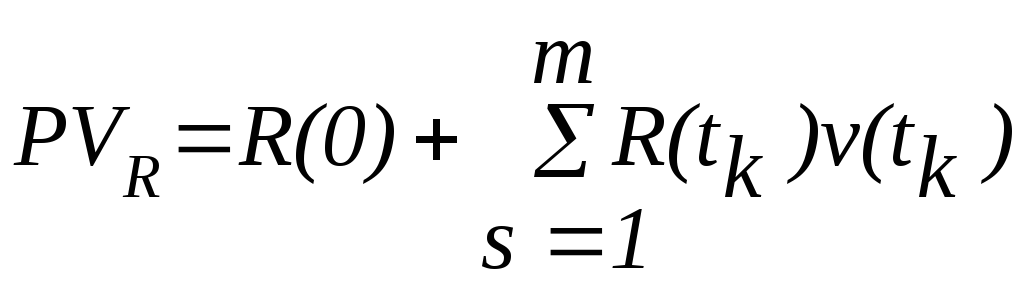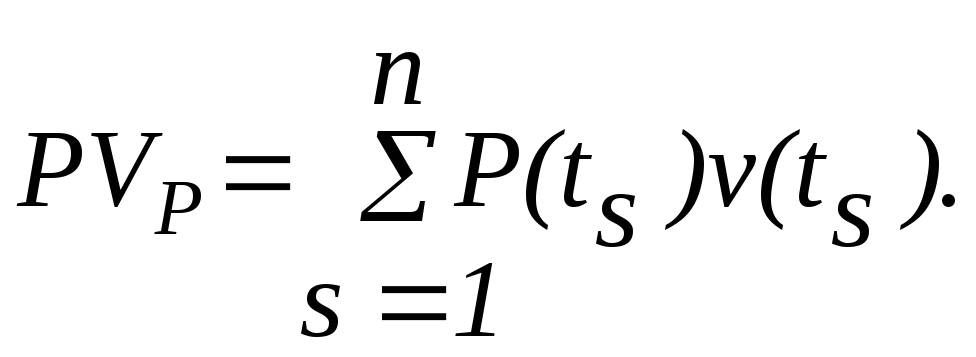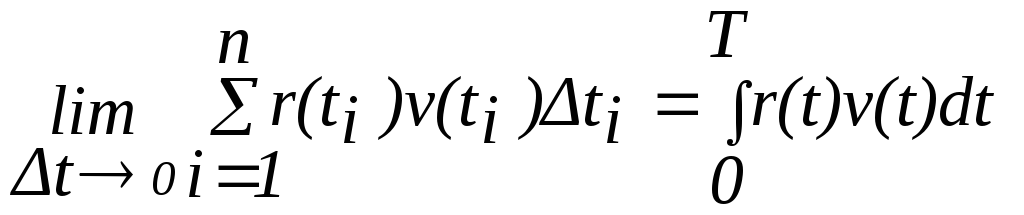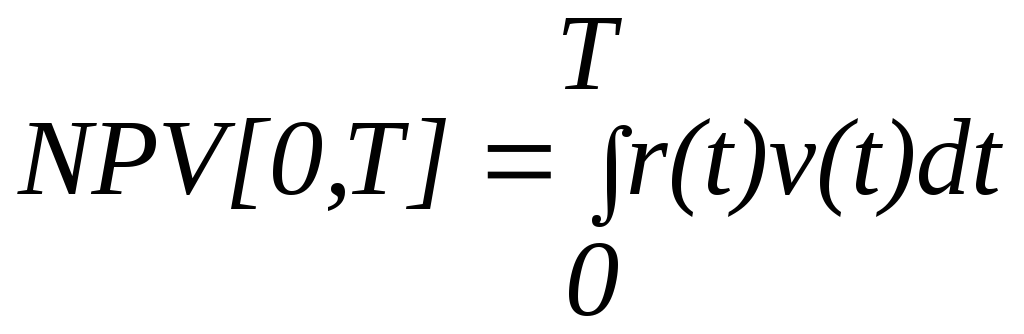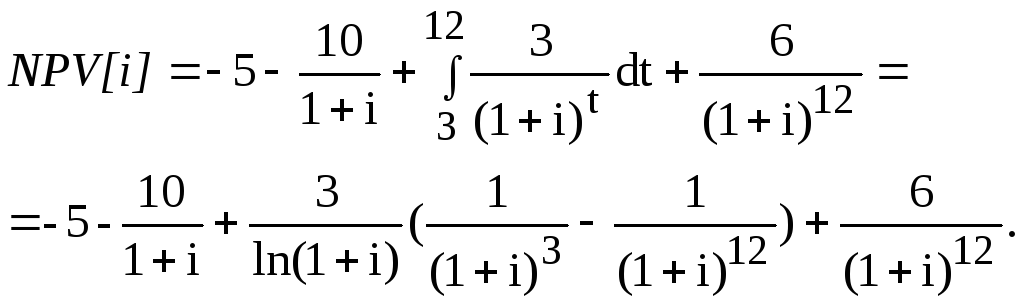Денежный поток в оценке стоимости

АНАЛИЗ ФИНАНСОВЫХ ПОТОКОВ

Виды денежных потоков в финансовой математике

Одним из основных элементов финансового анализа является оценка денежного потока , генерируемого в течение ряда временных периодов в результате реализации какого-либо проекта.

Определим следующие исходные условия:

• временные периоды предполагаются равными;

• элементы денежного потока являются однонаправленными, т. е. нет чередования оттоков и притоков денежных средств;

• денежные поступления не распределяются внутри периода, они сконцентрированы на одной из его границ.

Принято различать два вида денежных потоков:

• потоки, поступающие в начале каждого периода - потоки пренумерандо;

• потоки, поступающие в конце каждого периода - потоки постнумерандо.

Поток постнумерандо.

На практике большее распространение получил поток постнумерандо, поскольку оценка финансового результата проводится по окончании отчетного периода.

Поток пренумерандо имеет значение при анализе различных схем накопления денежных средств для последующего их инвестирования.

Оценка денежного потока может выполняться в рамках решения двух задач:

а) прямой, т. е. проводится оценка с позиции будущего (реализуется схема наращения);

б) обратной, т. е. проводится оценка с позиции настоящего (реализуется схема дисконтирования).

Временная оценка денежных потоков в оценке бизнеса

1. Функция «сложный процент».

2. Функция «дисконтирование».

3. Функция «текущая стоимость аннуитета».

4. Функция «периодический взнос на погашение кредита».

5. Функция «будущая стоимость аннуитета».

6. Функция «периодический взнос на накопление фонда».

7. Взаимосвязи между различными функциями.

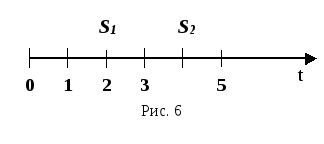
Приведение возникающих в разное время денежных сумм. Функции сложного процента. Функция «сложный процент» FV. Определение будущей стоимости суммы. Начисление сложного процента.

Функция «дисконтирование» PV. Определение настоящей стоимости суммы.

Функция «текущая стоимость аннуитета» PVA. Аннуитет. Исходящий и входящий денежный поток. Авансовый аннуитет.

Функция «периодический взнос на погашение кредита» PMT/PVA. Определение величины аннуитета.

Функция «будущая стоимость аннуитета» FVA. Величина накопленных равновеликих взносов.

Функция «периодический взнос на накопление фонда» PVA/FVA. Величина периодически депонируемой суммы.

Взаимосвязь функций при использовании базовой формулы сложного процента.

Выбор модели денежного потока при оценке стоимости бизнеса

Модели:

- для собственного капитала;

- для всего инвестированного капитала.

Денежный поток для собственного капитала =

Чистая прибыль после уплаты налогов

+ Амортизационные отчисления

+(-) Уменьшение (прирост) чистого оборотного капитала

+(-) Продажа активов (капитальные вложения)

+(-) Прирост (уменьшение) долгосрочной задолженности

Рассчитывается рыночная стоимость собственного (акционерного) капитала.

Денежный поток для всего инвестированного капитала =

Прибыль до уплаты процентов и налогов (EBIT)

- Налог на прибыль

+ Амортизационные отчисления

+(-) Уменьшение (прирост) чистого оборотного капитала

+(-) Продажа активов (капитальные вложения)

В обеих моделях поток может быть рассчитан как на номинальной основе (в текущих ценах), так и на реальной основе (с учетом фактора инфляции).

Если бизнес приносит изменяющийся поток доходов, то целесообразно использовать для его оценки:

а) метод избыточных прибылей;

б) метод капитализации дохода;

в) метод чистых активов;

г) метод дисконтирования денежных потоков?

8. Оценка стоимости собственного капитала методом чистых активов получается в результате:

а) оценки основных активов;

б) оценки всех активов компании;

в) оценки всех активов компании за вычетом всех ее обязательств;

г) ничего из вышеперечисленного.

9. Что является результатом суммирования чистого операционного дохода и предполагаемых издержек:

а) действительный валовой доход;

б) платежи по обслуживанию долга;

в) потенциальный валовой доход?

10. Что из нижеследующего не является компонентом метода кумулятивного построения при определении ставки дисконтирования:

а) безрисковая ставка;

б) премия за низкую ликвидность;

в) премия за риск;

г) премия за управление недвижимостью?

11. Какое из нижеследующих утверждений неправильно:

а) ставка капитализации для здания включает доход на инвестиции и возврат стоимости инвестиции;

б) общая ставка капитализации содержит доход на инвестиции и возврат самих инвестиций;

в) ставка капитализации для земли включает доход на инвестиции и возврат самих инвестиций?

12. Какой из подходов к оценке требует отдельной оценки стоимости земли:

а) сравнительный;

б) затратный;

в) доходный;

г) все перечисленные?

13. Существуют следующие виды износа (необходимо выбрать правильный ответ):

а) физическое устаревание, функциональное устаревание, внешний (экономический) износ;

б) физическое устаревание, функциональное устаревание, ускоренный износ;

в) устаревание окружающей среды, неустранимое устаревание, физическое устаревание, долгосрочный износ.

14. Определение стоимости гудвилла исчисляется на основе:

а) оценки избыточных прибылей;

б) оценки нематериальных активов;

в) оценки стоимости предприятия как действующего;

г) всего перечисленного;

д) а) и б).

15. Что из нижеследующего не является корректировками, применяемыми при оценке объекта методом сравнения продаж:

а) корректировка экономического коэффициента;

б) процентная корректировка;

в) корректировка по единицам сравнения;

г) долларовая корректировка?

16. Как рассчитывается валовой рентный мультипликатор:

а) делением цены продаж на потенциальный или действительный валовой доход;

б) делением чистого операционного дохода на цену продажи;

в) делением потенциального валового дохода на действительный и валовой доход;

г) делением действительного валового дохода на цену продаж?

17. В какую из статей обычно не вносятся поправки при корректировке баланса в целях определения стоимости чистых активов:

а) основные средства;

б) дебиторская задолженность;

в) запасы;

г) денежные средства?

18. Оценка стоимости миноритарного пакета акций компании открытого типа может быть получена при использовании:

а) метода сделок;

б) метода чистых активов;

в) метода дисконтирования денежных потоков;

г) метода рынка капитала.

Консолидация и замена платежей - финансовая математика

В реальной ситуации нередко одна из сторон коммерческой сделки обращается к другой с предложением изменить условия ранее заключенных соглашений.

Наиболее часто предлагается изменить сроки платежей в сторону их увеличения, произвести объединение нескольких платежей в один (консолидировать платежи) с установлением единого срока погашения.

Принцип, на котором базируется такое изменение контракта, называется принципом финансовой эквивалентности обязательств, который предполагает неизменность финансовых отношений сторон до и после изменения контракта.

Эквивалентными считаются такие платежи, которые, будучи приведены к одному моменту времени, оказываются равными. Рассмотрим рис. 6 S₁ и S₂ - суммы, приуроченные к моменту времени t = 2 и t = 4 соответственно.

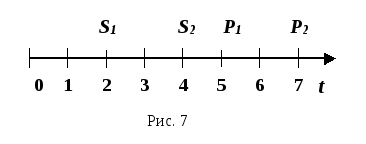
Приведем обе суммы S₁ и S₂ к начальному моменту времени по ставке приведения i, т.е. произведем дисконтирование этих сумм:

A₁ = S₁ (1 + i)^-2, A₂ = S₂ (1 + i)^-4.

Если A₁ = A₂ , то суммы S₁ и S₂ эквивалентны. Следовательно, замена суммы S₁ при t = 2 на сумму S₂ при t = 4 и наоборот, не изменит финансовых отношений сторон участников коммерческой сделки. Рассмотрим рис.7.

Здесь сравниваются два потока платежей: S₁ , S₂ и P₁, P₂ по сложной процентной ставке i. Для того чтобы заменить суммы S₁ и S₂ на две другие, эквивалентные по своим финансовым последствиям, суммы P₁ и P₂, применим принцип финансовой эквивалентности. Именно, приведем платежи S₁ и S₂ к начальному моменту времени (можно к любому другому) и сложим их:

S₁ (1 + i)^-2 + S₂ (1 + i)^-4 . (27)

То же самое проделаем с платежами P ₁ и P ₂:

P₁ (1 + i)^-5 + P₂ (1 + i)^-7. (28)

Приравнивая (27) и (28), получимуравнение эквивалентности:

S₁ (1 + i)^-2 + S₂ (1 + i)^-4 = P₁ (1 + i)^-5 + P₂ (1 + i)^-7. (29)

Очевидно, что данный метод распространяется на любое конечное число сумм. Если сравнение происходит по простой ставке i, то уравнение (29) примет вид:

S₁ (1 + 2i)^-1 + S₂ (1 + 4i)^-1 = P₁ (1 + 5i)^-1 + P₂ (1 + 7i)^-1.

В случае, когда несколько платежей S₁, S₂, S₃ со сроками n₁, n_2, n₃ соответственно, заменяются одним S₀ со сроком n₀, то уравнение эквивалентности в случае простых процентов запишется в виде:

S ₀ = S₁ (1 + (n₀ - n₁ )i) + S ₂ (1 + (n₀ - n₂ )i) + S₃ (1 + (n₀ - n₃ ) i),

если n ₀ >n₁, n₂, n₃. В другом случае, если n₁< n₀ <n₃, нужно применять как наращение (приn₀ > n_k), так и дисконтирование (n₀ < n_k).

Если проценты сложные, то, если n₁< n₀ <n₂ <n₃, уравнение эквивалентности примет вид (суммы приводятся к моменту n₀):

S₀ = S₁ (1 + i) + S₂ (1 + i) ^-() + S₃ (1 + i)^-() .

Пример. Два платежа - 1 и 0,5 млн руб. со сроками уплаты соответственно 150 и 180 дней - объединяются в один со сроком 200 дней. Определите консолидированную сумму долга, если стороны согласились на применение простой ставки, равной 20 %.

Решение. Приводя суммы 1 и 0,5 млн руб. к сроку n₀ = 200 дней, получим уравнение эквивалентности (К = 360):

S₀ = 1000 (1 + 0,2) + 500 (1 +0,2) = 1533,32 тыс. руб.

Пример. Имеется два кредитных обязательства - 500 тыс. руб. и 600 тыс. руб. со сроками уплаты 01.10 и 01.01 (нового года).

По согласованию сторон обязательства были пересмотрены на новые условия: первый платеж в размере 700 тыс. руб. должник вносит 01.02, остальной долг он выплачивает 01.04. Ставка сравнения 10 % простая. Рассчитайте величину второго платежа S₀.

Решение. За дату приведения примем 01.01 (нового года), К = 360. Учитывая, что 01.10 - 274-й порядковый день в году, 01.02 - 32-й день, 01.04 - 91-й день, запишем уравнение эквивалентности:

500 (1 + 0,1) + 600 = 700 (1 +0,1)^-1 + S ₀ (1 + 0,1)^-1.

Решая это уравнение относительно S₀, находим:S₀ = 409,417 тыс. руб.

Задачи

7.1. Долг в размере 300 тыс. руб. должен быть выплачен через два года. Найдите эквивалентные значения для этой суммы (ставка сравнения 25 %):

а) в конце первого года,

б) через 5 лет.

Ответ: а) 240 тыс. руб.; б) 585,938 тыс. руб.

7.2. Вычислите эквивалентное значение долга, которого он достигнет через два года, если в настоящее время он составляет 42 тыс. руб. Проценты начисляются поквартально по ставке 40 % годовых. Ответ:90,031 тыс. руб.

7.3. Исходный поток платежей составляет: 200 тыс. руб. - через один год, 175 тыс. руб. - через два года, 210 тысяч руб. - через 4 года. Замените его эквивалентным множеством, состоящим из двух выплат, равных по величине, первая из которых осуществляется через 1,5 года, а вторая - через 4 года. Проценты начисляются по ставке 8 % годовых каждые полгода.

7.4. Долг должен быть погашен двумя платежами: 100 тыс. руб. через один год и 370 тыс. руб. через три года. Определите срок, при котором замена обеих выплат одной, в размере 480 тыс. руб., будет эквивалентной при ставке – 15 % годовых.

7.5. По условиям контракта, заключенного 01.02, за полученные в кредит товары фирма должна заплатить через 120 дней - 1,5 млн руб., а затем через 240 дней еще 1,2 млн руб. Достигнуто соглашение с кредитором об изменении условий контракта. Платежи производятся равными суммами: первый платеж - через 90 дней, второй - через 180 дней. При расчете применяется простая ставка 10 % годовых. Определите величину каждого платежа. Ответ: 1,3361 млн руб.

7.6. Строительная фирма получила в банке долгосрочный кредит в размере 5 млн. руб. под 6 % годовых (проценты сложные), срок погашения - через 5 лет. Впоследствии стороны пересмотрели условия займа и выработали новые: через три года производится выплата 3 млн. руб., остальная сумма выплачивается через 4 года. Процентная ставка сохраняется прежней. Определите сумму окончательного платежа.

7.7. Заемщик должен уплатить кредитору 10 млн руб. через 5 лет. Стороны согласились изменить условия погашения долга: через 2 года выплачивается 3 млн руб., а оставшийся долг спустя 4 года после первой выплаты. Определите сумму окончательного платежа, если сложная процентная ставка равна 10 % годовых.

Модель дискретного потока платежей - финансовая математика

Рассмотрим модель детерминированного дискретного потока денежных расходов (капитальных вложений) и поступлений в инвестиционном процессе.

Пусть инвестиционный проект начинается в момент t=0 с капвложения R(0) рублей. Затем в моменты t_k происходят инвестиции в размере R(t_k ) или доходы в размере P(t_S ) руб.

Определение. Современной стоимостью PV (Present Value) потока платежей называется сумма приведенных к моменту t=0 величин этих платежей. В нашем случае современные стоимости инвестиций и доходов вычисляются cоответственно по формулам:

Здесь V(t_k) = (1+i)^-t_k - коэффициент приведения (дисконтирования).

Определение. Чистым приведенным доходом NPV (Net Present Value) называется алгебраическая сумма всех платежей, приведенных к моменту t=0 по ставке процента i:

NPV = VP_P - PV_R .

Чистый приведенный доход характеризует общий абсолютный результат инвестиционной деятельности. Ставка процентов, по которой производится дисконтирование, называется ставкой сравнения или спот-ставкой.

Модель непрерывного потока платежей - финансовая математика

В коммерческой практике встречается случай, когда фирме приходится производить частые, но небольшие денежные расходы и поступления. Если баланс финансового потока подсчитывается также часто, то такие платежи при теоретическом финансовом анализе можно описать с помощью модели непрерывного потока платежей. Пусть на временном отрезке [0,T] расходы и доходы поступают с интенсивностью R(t) руб/год. На отрезке [t, t+?t] величина потока платежей составит R(t) ?t руб. Приведенная величина этого потока на момент t = 0 на данном отрезке ? R(t) V(t) ?t, где V(t)=(1+i)^-t. Суммируя по всему отрезку [0,T] и переходя к пределу при ?t ? ?, получим:

Следовательно, чистый приведенный доход на отрезке [0,T] равен

Данная модель позволяет анализировать те этапы инвестиционного проекта, когда не было значительных вложений или поступлений.

Пример. Рассмотрим инвестиционный проект, реализация которого потребует Т=12 лет и предполагает следующий дискретно-непрерывный поток платежей (десятки. тыс. долл.):

С(0) = ?5; С(1) = ? 10; С(12) = 6; r(t) = 3 при 3 ? t ? 12.

Найти NPV данного проекта при ставках сравнения i = 10 % и 15 %.

Решение.

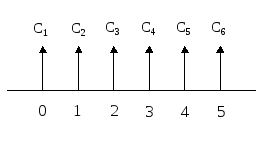
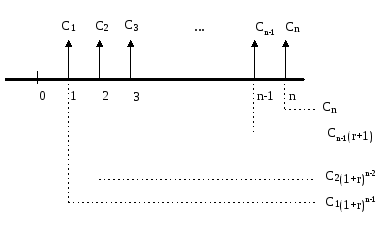
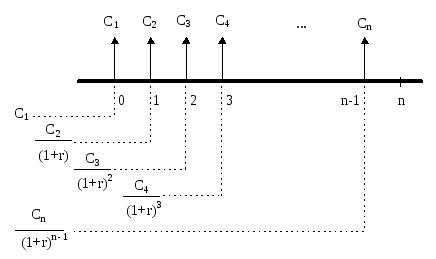
NPV(10 %) = 1,44; NPV(15 %) = - 2,47.

Оценка денежного потока с неравными поступлениями в финансовой математике

Оценка потока постнумерандо.

Будущая стоимость исходного денежного потока постнумерандо.

. (17)

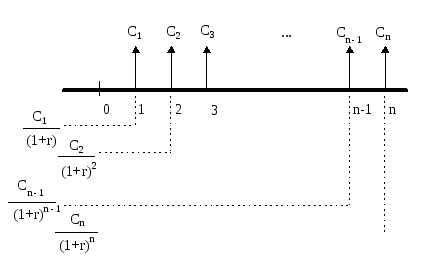
Рис. 3. Логика решения прямой задачи для потока постнумерандо.

Приведенная стоимость денежного потока постнумерандо.

. (18)

Рис. 4. Логика решения обратной задачи для потока постнумерандо.

Пример 17.

Рассчитать приведенную стоимость денежного потока постнумерандо (тыс. руб.): 12, 15, 9, 25, если коэффициент дисконтирования r = 12 %.

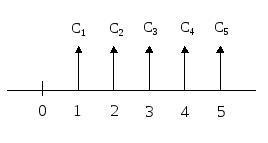
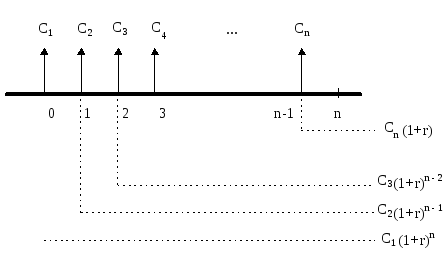
= 12 · 0,8929 + 15 · 0,7972 + 9 · 0,7118 + 25 · 0,6355 =

= 10,71 + 11,96 + 6,41 + 15,89 = 44,97 тыс. руб.

Оценка потока пренумерандо.

Будущая стоимость денежного потока пренумерандо.

, (19)

.

Рис. 5. Логика решения прямой задачи для потока пренумерандо.

Приведенная стоимость денежного потока пренумерандо.

. (20)

Рис. 6. Логика решения обратной задачи для потока пренумерандо.

Пример 18.

Исходные данные из примера 17, при условии, что исходный поток представляет собой пренумерандо.

= 44,97 · 1,12 = 50,37 тыс. руб.

Оценка денежных потоков от недвижимости в доходном подходе

Показатель	Период
	прогнозный, номер квартала					пост- прогноз-ный, год
	1	2	3	4	5	6
Ремонтные работы, тыс.руб.	4400,0	4400,0	-	-	-
Поступле-ние чистой арендной платы, тыс.руб.			1368,0* при 40%-й загрузке здания	2736,0** при 80%-й загрузке здания	3249,0*** при 95%-й загрузке здания	10944****
Денежный поток от вложений и аренды, тыс.руб.	-4400,0	-4400,0	1368,0	2736,0	3249,0	10944
Коэффици-ент капита-лизации для постпрогно-зного периода						0,16*****
Стоимость реверсии******, тыс.руб.					68400
Денежный поток от вложений и аренды с учетом стоимости реверсии, тыс.руб.	-4400,0	-4400,0	1368,0	2736,0	71649,0
Дисконтиру-ющий множитель при ставке дисконта 14%	0,966	0,934	0,902	0,871	0,842

Окончание табл.50

Показатель	Период
	прогнозный, номер квартала					пост- прогноз-ный, год
	1	2	3	4	5	6
Дисконтиро-ванный денежный поток, тыс.руб.	-4250	-4110	1234	2383	60328,5
Сумма дисконтиро-ванных денежных потоков, тыс.руб.	55585,5

*1900кв.м*0,600 тыс.руб.*3 месяца*0,4 = 1368,0 тыс.руб.

**1900кв.м*0,600 тыс.руб.* 3 месяца*0,8 = 2736,0 тыс.руб.

***1900кв.м*0,600 тыс.руб.* 3 месяца*0,95 = 3249,0 тыс.руб.

****1900кв.м*0,600 тыс.руб.* 12 месяцев*0,8 = 10944,0 тыс.руб.

*****Находим методом суммирования по формуле (51). Предполагаем, что срок экономической жизни составляет 50 лет. По методу Ринга норма возврата капитала составит 2%. Таким образом, сумма нормы прибыли и нормы возврата капитала равна 16%.

******Расчет стоимости реверсии производим, капитализируя ЧОД в постпрогнозный период по ставке капитализации 16%.

Ответ: V= 55585,5 тыс.руб.

Оценка денежных потоков от объекта недвижимости

Показатель	Период
	прогнозный, номер квартала						пост- прогноз-ный, год
	1	2	3	4	5	6
Ремонтные работы, тыс.руб.	4400,0	4400,0	-	-	-
Поступле-ние чистой арендной платы, тыс.руб.			1368,0* при 40%-й загрузке здания	2736,0** при 80%-й загрузке здания	3249,0*** при 95%-й загрузке здания	10944****
Денежный поток от вложений и аренды, тыс.руб.	-4400,0	-4400,0	1368,0	2736,0	3249,0	10944
Коэффици-ент капита-лизации для постпрогно-зного периода						0,16*****
Стоимость реверсии******, тыс.руб.					68400
Денежный поток от вложений и аренды с учетом стоимости реверсии, тыс.руб.	-4400,0	-4400,0	1368,0	2736,0	71649,0
Дисконтиру-ющий множитель при ставке дисконта 14%	0,966	0,934	0,902	0,871	0,842

Окончание табл.50

Показатель	Период
	прогнозный, номер квартала						пост- прогноз-ный, год
	1	2	3	4	5	6
Дисконтиро-ванный денежный поток, тыс.руб.	-4250	-4110	1234	2383	60328,5
Сумма дисконтиро-ванных денежных потоков, тыс.руб.	55585,5

*1900кв.м*0,600 тыс.руб.*3 месяца*0,4 = 1368,0 тыс.руб.

**1900кв.м*0,600 тыс.руб.* 3 месяца*0,8 = 2736,0 тыс.руб.

***1900кв.м*0,600 тыс.руб.* 3 месяца*0,95 = 3249,0 тыс.руб.

****1900кв.м*0,600 тыс.руб.* 12 месяцев*0,8 = 10944,0 тыс.руб.

*****Находим методом суммирования по формуле (51). Предполагаем, что срок экономической жизни составляет 50 лет. По методу Ринга норма возврата капитала составит 2%. Таким образом, сумма нормы прибыли и нормы возврата капитала равна 16%.

******Расчет стоимости реверсии производим, капитализируя ЧОД в постпрогнозный период по ставке капитализации 16%.

Ответ: V= 55585,5 тыс.руб.

Приведенная к настоящему моменту стоимость будущих денежных потоков в финансовой математике

; (16)

; .

Выражение называетсякоэффициентом текущей стоимости (present value factor).

Пример 14.

Какую сумму необходимо поместить в банк, чтобы через три года получить 10 000 $ при ставке дисконта 10 %?

.

Правило сложения текущих стоимостей.

Текущая стоимость любого набора денежных потоков равна сумме текущих стоимостей каждого из денежных потоков.

;

.

Пример 15.

Корпорация ожидает получить от инвестиционного проекта следующие притоки реальных денег в будущем: 1 год - 2000$, 2 год - 3000$, 3 год - 4000$, 4 год - 6000$.

Требуется определить продуктивную ценность при ставке дисконта 14 %.

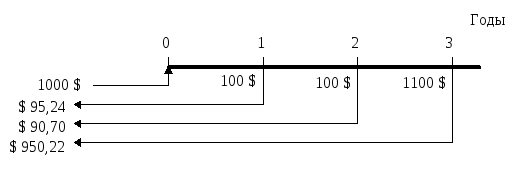
= 2000 · 0,877193 + 3000 · 0,769468 + 4000 · 0,674972 + 6000 · 0,59208 =

=1754 + 2308 + 2700 + 3552 = 10314 $.

Пример 16.

Вкладчик инвестирует 1000 $ с получать в качестве процентов ежегодно 100 $. В конце третьего года он кроме 100 $ получает первоначальную сумму вклада. Ставка дисконта 5 %. Определить приведенную стоимость инвестиции.

.

Правило умножения текущих стоимостей.

Коэффициент текущей стоимости за n лет равен произведению коэффициента дисконтирования стоимости за t лет и коэффициента дисконтирования стоимости за (n - t) лет.

Например, при 8 %-й ставке дисконтирования коэффициент текущей стоимости 1 $, получаемого через 3 года равен , а для 1 $, получаемого через 9 лет. Следовательно, текущая стоимость 1 $ через 12 лет (t = 3; n = 12; (n - t) = 9) равна: 0,7938 · 0,5002 = 0,3971.

Проверка: .

.

Прогнозирование и оценка величин денежных потоков от объекта недвижимости

Расчет различных уровней дохода от объекта недвижимости можно представить формулами:

ПВД = Площадь ? Ставка арендной платы (4.28)

ДВД = ПВД – Потери от незанятости и при сборе арендной платы + Прочие доходы (4.29)

ЧОД = ДВД – Операционные расходы владельца недвижимости, связанные с недвижимостью (4.30)

На практике российские оценщики рассчитывают чистые денежные потоки объекта недвижимости без учета особенностей финансирования, т.е. в методе ДДП дисконтируются величины чистого операционного дохода.

При оценке рыночной стоимости объекта недвижимости в качестве денежного потока выступает чистый операционный доход от объекта недвижимости.

Однако если необходимо оценить инвестиционную стоимость объекта недвижимости или стоимость при существующем использовании, то необходимо учитывать фактические расходы собственника или инвестора, следовательно, используются следующие уровни денежных потоков:

Денежный поток до уплаты налогов = ЧОД – Капиталовложения – Обслуживание кредита + Прирост кредитов. (4.31)

Денежный поток для недвижимости после уплаты налогов =

= Денежный поток до уплаты налогов – Платежи по подоходному налогу владельца недвижимости. (4.32)

Налог на землю и налог на имущество необходимо вычитать из действительного валового дохода в составе операционных расходов.

Экономическая и налоговая амортизация не является реальным денежным платежом, поэтому амортизация не входит в состав операционных расходов собственника.

Капитальные вложения, осуществляемые для поддержания оцениваемого объекта, необходимо вычитать из чистого операционного дохода в составе операционных расходов.

Платежи по обслуживанию кредита (выплата процентов и погашение долга) необходимо вычитать из чистого операционного дохода, если оценивается инвестиционная стоимость объекта (для конкретного инвестора).

Расчет величины денежного потока в прогнозном периоде при оценке бизнеса предприятия

При оценке бизнеса мы можем применять одну из двух моделей денежного потока:

•ДП для собственного капитала

•ДП для всего инвестированного капитала.